1) Giải hệ phương trình .
2) Giải phương trình x2 + x – 6 = 0.
3) Giải phương trình x4 – x2 – 12 = 0.
1) Giải hệ phương trình .
2) Giải phương trình x2 + x – 6 = 0.
3) Giải phương trình x4 – x2 – 12 = 0.
Câu hỏi trong đề: Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
1)
Û
Vậy hệ phương trình đã cho có nghiệm là (2; 3).
2) x2 + x – 6 = 0
Û x2 – 2x + 3x – 6 = 0
Û x(x – 2) + 3(x – 2) = 0
Û (x – 2)(x + 3) = 0
Û
Û .
Vậy tập phương trình đã cho là S = {2; −3}.
3) x4 – x2 – 12 = 0 (1)
Đặt t = x2 (t ≥ 0), phương trình (1) trở thành:
t2 – t – 12 = 0
Û t2 + 3t – 4t – 12 = 0
Û t(t + 3) – 4(t + 3) = 0
Û (t – 4)(t + 3) = 0
Û t – 4 = 0 hay t + 3 = 0
Û t = 4 (nhận) hay t = −3 (loại)
Ta có: x2 = 4 Û x = 2 hay x = −2.
Vậy tập phương trình đã cho là S = {2; −2}.
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
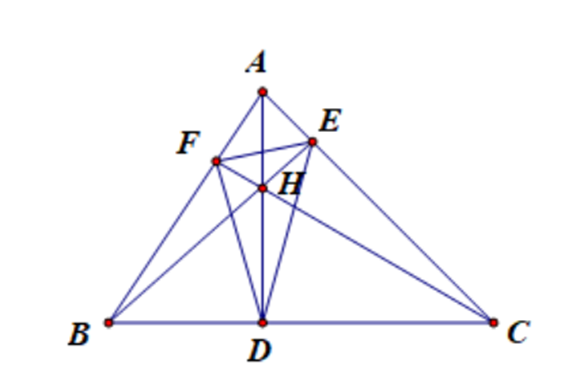
1) Xét tứ giác AEHF, có mà hai góc ở vị trí đối nhau.
Vậy tứ giác AEHF nội tiếp
2) Xét tứ giác BFEC, có: mà hai góc cùng nhìn cạnh BC.
Suy ra tứ giác BFEC nội tiếp.
Do đó .
Vậy .
3) Tam giác ABC có BE ^ AC; CF ^ AB, BE và CF cắt nhau tại H.
Suy ra H là trực tâm tam giác ABC nên AH ^ BC tại D.
Khi đó
Do đó tứ giác BFHD và CEHD nội tiếp.
+ Tứ giác AEHF nội tiếp Þ Þ
Tứ giác CDHE nội tiếp Þ Þ
Mà (cùng phụ )
Þ Þ EH là phân giác góc DEF.
+ Tứ giác AEHF nội tiếp Þ Þ
Tứ giác BFHD nội tiếp Þ Þ
Mà (cùng phụ )
Þ
Þ FH là phân giác góc DFE
Mà FH và EH cắt nhau tại H
Þ H là tâm đường tròn nội tiếp tam giác DEF.
Lời giải
1) x2 – 6x + m = 0 (a = 1, b = −6, c = m)
Ta có: ∆ = b2 – 4ac = (−6)2 – 4.1.m = 36 – 4m
Để phương trình có nghiệm kép thì ∆ = 0 Û 36 – 4m = 0
Û 4m = 36 Û m = 9.
Thay m = 9 vào phương trình trên ta được:
x2 – 6x + 9 = 0
Û (x – 3)2 = 0 Û x = 3.
Vậy để phương trình đã cho có nghiệm kép thì m = 9 và nghiệm kép là x = 3.
2) x2 – 3x – 2 = 0 (a = 1, b = −3, c = −2)
Theo hệ thức Vi – ét, ta có:
Ta có: P = x12 + x22 = (x1 + x2)2 − 2x1x2 = 32 – 2.(−2) = 13.
Vậy P = x12 + x22 = 13.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo