a) Tính diện tích của một mặt cầu, biết bán kính của mặt cầu đó bằng 6 cm.
b) Biết một hình nón có bán kính đường tròn đáy là 8 cm và độ dài đường sinh là 17 cm. Tính thể tích của hình nón đó.
a) Tính diện tích của một mặt cầu, biết bán kính của mặt cầu đó bằng 6 cm.
b) Biết một hình nón có bán kính đường tròn đáy là 8 cm và độ dài đường sinh là 17 cm. Tính thể tích của hình nón đó.
Câu hỏi trong đề: Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Ta có công thức tính diện tích mặt cầu là S = 4p.R3
Thay R = 6cm vào S, ta được:
4p.63 = 864p (cm2).
Vậy diện tích của một mặt cầu cần tìm là 864p cm2.
b) Ta có Rđáy = 
= 4 cm.
Chiều cao hình nón là:
h = = = (cm)
Thể tích hình nón là:
V = pR2.h = p.42. ≈ 276,8 (cm3).
Vậy thể tích của hình nón khoảng 276,8 cm3.
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a)
Cộng phương trình (1) và (2) vế theo vế ta được:
7x = 14 Û x = 2.
Thay x = 2 vào phương trình (1) ta được: 4.2 – y = 5 Û y = 3.
Vậy hệ phương trình có nghiệm là (2; 3).
b) x2 + 4x – 5 = 0
Û x2 – x + 5x – 5 = 0
Û x(x – 1) + 5(x – 1) = 0
Û (x + 5).(x – 1) = 0
Û Û .
Vậy tập nghiệm của phương trình đã cho là S = {1; −5}.
Lời giải
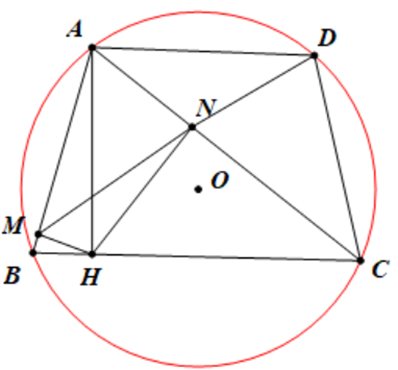
a) Ta có: HM ^ AB Þ
HN ^ AC Þ
Xét tứ giác AMHN có = 90° + 90° = 180°.
Mà hai góc nằm ở vị trí đối nhau.
Do đó tứ giác AMHN nội tiếp.
b) Ta có (chứng minh trên)
Suy ra = = 90°
Mà = 90° (∆HNC có = 90°)
Nên hay
Mà
Do đó .
c) Ta có
Suy ra = 180° hay = 180°
Do đó tứ giác BMNC nội tiếp.
Suy ra = 180° hay = 180°
Mà tứ giác ADCB nội tiếp đường tròn (O) nên = 180°.
Suy ra mà (hai góc đối đỉnh)
Do đó
Xét ∆AND và ∆ADC có:
chung
(cmt)
Do đó ∆AND 
∆ADC (g.g)
Suy ra
Do đó AD2 = AN.AC (đpcm).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo