Cho tam giác ABC cân tại A. Vẽ AH vuông góc BC tại H
Trên cạnh AB lấy điểm D (D nằm giữa N và B, và trên tia đối tia CA lấy điểm E sao cho BD=CE. Đường thẳng qua C song song với DE và đường thẳng qua D song song với AC cắt nhau tại F. Chứng minh tam giác DFB cân và
Câu hỏi trong đề: Trắc nghiệm bài tâp theo tuần Toán 7-Tuần 32 có đáp án !!
Quảng cáo
Trả lời:
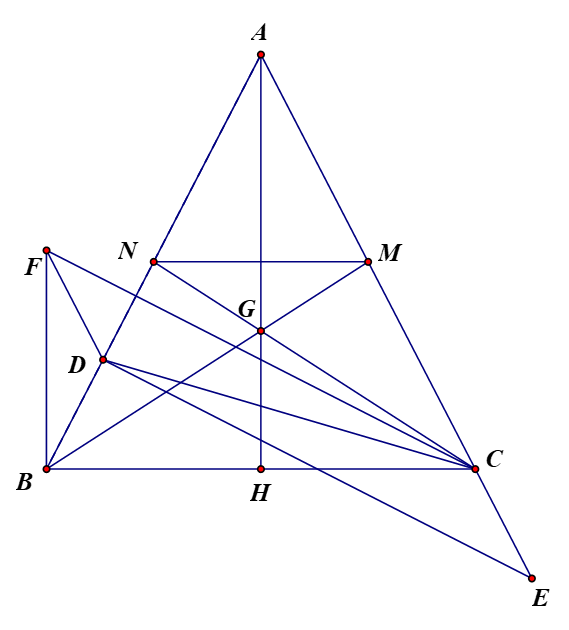
Chứng minh
Nên và
Chứng minh tam giác DFB cân tại D (vì )
Ta có và
Mà (góc đáy tam giác cân)
Ta có (góc ngoài tam giác)
Mà nên
Cho nên .
Vậy (quan hệ góc và cạnh đối diện)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
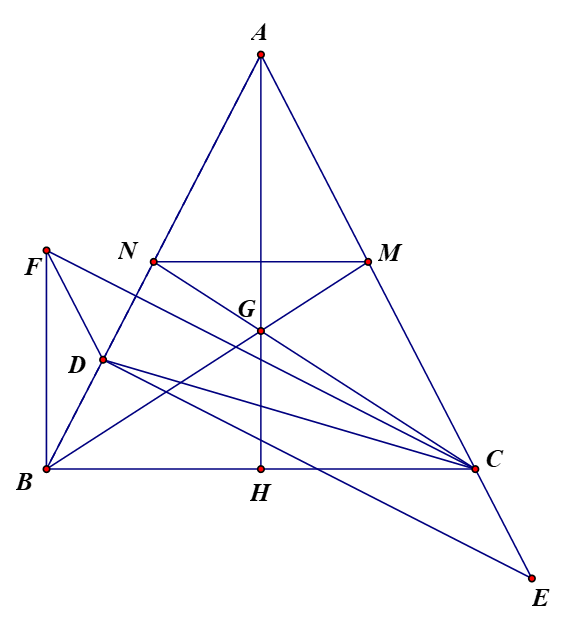
Xét tam giác và tam giác có
(tam giác ABC cân tại A)
AH cạnh chung
Góc góc (AH vuông góc BC)
(cạnh huyền-cạnh góc vuông)
Nên
Lời giải
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Điểm kiểm tra 1 tiết môn toán của học sinh lớp 7A được ghi lại ở bảng sau:
|
5 |
8 |
6 |
8 |
7 |
8 |
10 |
7 |
8 |
5 |
|
5 |
6 |
8 |
7 |
6 |
7 |
5 |
7 |
10 |
8 |
|
7 |
8 |
9 |
6 |
8 |
10 |
8 |
7 |
6 |
8 |
|
8 |
9 |
7 |
8 |
6 |
4 |
5 |
8 |
9 |
7 |
Lập bảng tần số và tính số trung bình cộng của dấu hiệu
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.