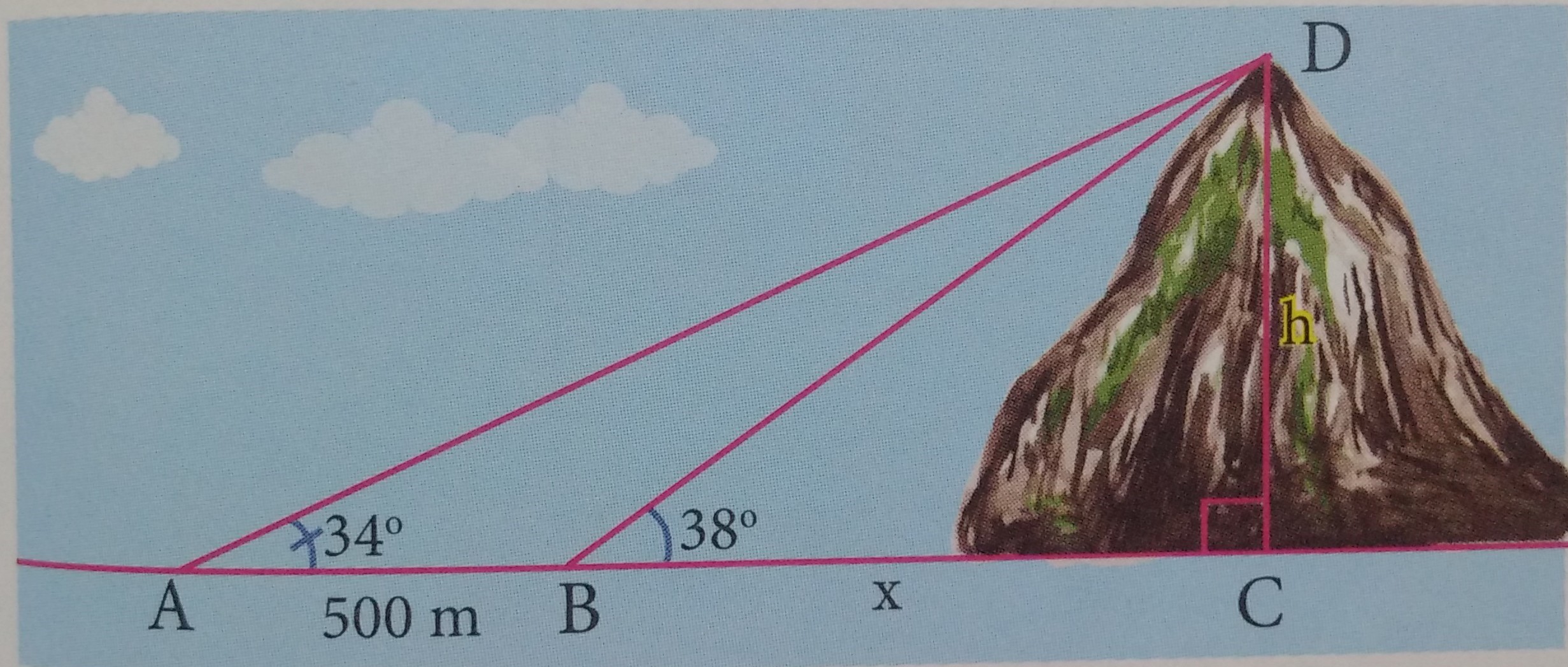
Quãng đường đi của một vật rơi tự do không vận tốc đầu cho bởi công thức S=12gt2 (trong đó g là gia tốc trọng trường g≈9,8m/s2, t là thời gian rơi tự do, S là quãng đường rơi tự do). Một vận động viên...

Quãng đường vận động viên nhảy từ vị trí A đến vị trí B là: S=3500−1500=2000m Thay S = 2000 vào công thức S=12gt2, ta được: 2000=12.9,8.t2⇒t2=40009,8⇒t=40009,8≈20,2 giây Vậy vận động viên phải mở dù sau thời gian 20,2 giây.

Câu hỏi:

13/07/2024 29,345

Quãng đường đi của một vật rơi tự do không vận tốc đầu cho bởi công thức $S = \frac{1}{2} {gt}^{2}$ (trong đó g là gia tốc trọng trường $g \approx {9,8m/s}^{2}$ , t là thời gian rơi tự do, S là quãng đường rơi tự do). Một vận động viên nhảy dù, nhảy khỏi máy bay ở độ cao 3500 mét (vị trí A) với vận tốc ban đầu không đáng kể. Hỏi sau thời gian bao nhiêu giây (làm tròn đến chữ số thập phân thứ nhất) vận động viên phải mở dù để khoảng cách từ (vị trí B) đến mặt đất (vị trí C) trong hình vẽ là 1500 mét.

Xem lời giải

Câu hỏi trong đề: Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

Quãng đường vận động viên nhảy từ vị trí A đến vị trí B là: $S = 3500 - 1500 = 2000m$

Thay S = 2000 vào công thức $S = \frac{1}{2} {gt}^{2}$ , ta được:

$2000 = \frac{1}{2} {.9,8.t}^{2} \Rightarrow t^{2} = \frac{4000}{9,8} \Rightarrow t = \sqrt{\frac{4000}{9,8}} \approx 20,2$ giây

Vậy vận động viên phải mở dù sau thời gian 20,2 giây.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
Đăng ký ngay

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một chiếc thang dài 3m. Cần đặt chân thang cách chân tường một khoảng cách bằng bao nhiêu để nó tạo với mặt đất một góc “an toàn” 65⁰ (tức đảm bảo thang không bị đổ khi sử dụng)? (kết quả làm tròn đến chữ số thập phân thứ 2)

Xem đáp án

Lời giải

Theo đề bài ta có hình vẽ sau:

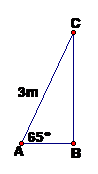
Media VietJack

$\begin{array}{l} \cos \hat{C A B} = \cos 65^{0} = \frac{A B}{A C} = \frac{A B}{3} \end{array}$ $\Rightarrow A B = 3. \cos 65^{0} \approx 1, 27 (m)$

Vậy: Cần đặt chân thang cách chân tường một khoảng 1,27 m

Câu 2

Hai dung dịch muối có khối lượng tổng cộng bằng 220 kg. Lượng muối trong dung dịch I là 5kg, lượng muối trong dung dịch II là 4,8kg. Biết nồng độ muối trong dung dịch I nhiều hơn nồng độ muối trong dung dịch II là 1% Tính khối lượng mỗi dung dịch nói trên.

Xem đáp án

Lời giải

Gọi

x, y (kg) (220 > x > 0 ; 220 > y > 0)

lần lượt là khối lượng dung dịch I và dung dịch II.
Theo đề ta có:

x + y = 220 (1)

Nồng độ muối trong dung dịch I là:

\frac{5}{x} .100 = \frac{500}{x} (%)

Nồng độ muối trong dung dịch II là:

\frac{4, 8}{y} .100 = \frac{480}{y} (%)

Vì nồng độ muối trong dung dịch I nhiều hơn nồng độ muối trong dung dịch II nên:

\frac{500}{x} - \frac{480}{y} = 1 (2)

Từ (1) và (2), ta có hệ phương trình:

\{\begin{cases} x + y = 220 \\ \frac{500}{x} - \frac{480}{y} = 1 \end{cases} \Leftrightarrow \{\begin{cases} y = 220 - x \\ \frac{500}{x} - \frac{480}{220 - x} = 1 (*) \end{cases}

Ta có:

(*) \Leftrightarrow 500 (220 - x) - 480 x = x (220 - x)

\begin{array}{l} \Leftrightarrow 110000 - 500 x - 480 x = 220 x - x^{2} \\ \Leftrightarrow x^{2} - 1200 x + 110000 = 0 \end{array}

\begin{array}{l} Δ = b^{2} - 4 a c = {(- 1200)}^{2} - 4.1.110000 = 1000000 \\ \sqrt{Δ} = 1000 \\ x_{1} = \frac{- b - \sqrt{Δ}}{2 a} = \frac{- (- 1200) - 1000}{2} = 100 (n) \\ x_{2} = \frac{- b + \sqrt{Δ}}{2 a} = \frac{- (- 1200) + 1000}{2} = 1100 (l) \end{array}

Với

x = 100 \Rightarrow y = 220 - x = 120 (n)

Vậy khối lượng dung dịch I là 100kg và khối lượng dung dịch II là 120kg .

Câu 3

Tốc độ tăng trưởng dân số bình quân hàng năm có thể tính theo công thức:
$\bar{r} = \sqrt{\frac{P_{t}}{P_{0}}} - 1$

        Trong đó:

                : Dân số thời điểm gốc

                : Dân số thời điểm năm sau

                : Tốc độ tăng trưởng dân số bình quân hàng năm.

Tổng số dân Việt Nam năm 2014 là 90728,9 ngàn người. Tổng số dân Việt Nam năm 2015 là: 91703,8 ngàn người.

a) Hãy tính tốc độ tăng trưởng dân số bình quân hàng năm của Việt Nam trong giai đoạn trên.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Một chiếc máy bay bay lên với vận tốc 600km/h. Đường bay lên tạo với phương nằm ngang một góc 35⁰ (hình bên). Hỏi sau 1 phút máy bay lên cao được bao nhiêu km theo phương thẳng đứng? (làm tròn kết quả đến số thập phân thứ 2)

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Tính chiều cao của một ngọn núi (làm tròn đến mét), biết tại hai điểm A, B cách nhau 500m, người ta nhìn thấy đỉnh núi với góc nâng lần lượt là 34^o và 38^o.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Bác Xuân vay 20.000.000 đồng của ngân hàng để làm kinh tế. Trong một năm đầu bác chưa trả được nên số tiền lãi trong năm đầu được chuyển thành vốn để tính lãi năm sau. Sau 2 năm bác An phải trả là 23.540.000 đồng. Hỏi lãi suất cho vay là bao nhiêu phần trăm trong một năm đầu? Biết rằng trong năm sau ngân hàng đã giảm 30% lãi suất.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

V-ACT

HSA

TSA

SPT

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Một chiếc máy bay bay lên với vận tốc 600km/h. Đường bay lên tạo với phương nằm ngang một góc 35⁰ (hình bên). Hỏi sau 1 phút máy bay lên cao được bao nhiêu km theo phương thẳng đứng? (làm tròn kết quả đến số thập phân thứ 2)

Tính chiều cao của một ngọn núi (làm tròn đến mét), biết tại hai điểm A, B cách nhau 500m, người ta nhìn thấy đỉnh núi với góc nâng lần lượt là 34^o và 38^o.