Câu hỏi:
13/07/2024 1,318
Có các con đường nối bốn ngôi làng A, B, C, D như trong Hình 5. Có bao nhiêu cách chọn đường đi khác nhau
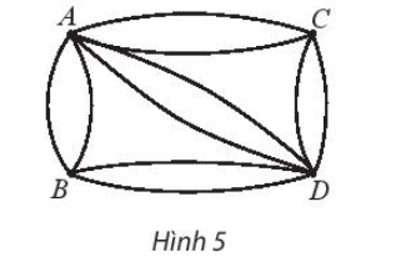
a) từ A qua B rồi đến D?
Có các con đường nối bốn ngôi làng A, B, C, D như trong Hình 5. Có bao nhiêu cách chọn đường đi khác nhau
a) từ A qua B rồi đến D?
Câu hỏi trong đề:
Giải SBT Toán 10 Bài 1. Quy tắc cộng và quy tắc nhân có đáp án !!
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Việc đi từ A qua B rồi đến D bao gồm hai công đoạn:
Công đoạn 1: Đi từ A đến B có 2 cách chọn.
Công đoạn 2: Ứng với mỗi cách chọn đường đi từ A đến B có 2 cách chọn đường đi từ B đến D.
Áp dụng quy tắc nhân, ta có 2.2 = 4 cách chọn con đường từ A qua B rồi đến D.
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Tung đồng thời hai con xúc xắc khác nhau và ghi lại số chấm xuất hiện trên mỗi con xúc xắc. Có bao nhiêu kết quả có thể xảy ra mà tổng số chấm xuất hiện trên hai mặt là bội của 5?
Tung đồng thời hai con xúc xắc khác nhau và ghi lại số chấm xuất hiện trên mỗi con xúc xắc. Có bao nhiêu kết quả có thể xảy ra mà tổng số chấm xuất hiện trên hai mặt là bội của 5?
Xem đáp án »
13/07/2024
5,963
Câu 2:
Sử dụng 5 chữ số 0; 1; 2; 3; 4 có thể lập được bao nhiêu số tự nhiên
a) có ba chữ số khác nhau?
Sử dụng 5 chữ số 0; 1; 2; 3; 4 có thể lập được bao nhiêu số tự nhiên
a) có ba chữ số khác nhau?
Xem đáp án »
13/07/2024
3,827
Câu 3:
Mã số nhân viên của một công ty có 4 kí tự, gồm một chữ cái đầu tiên (từ 6 chữ cái A, B, C, D, E, F) và tiếp theo là 3 chữ số (từ các chữ số 0; 1;...; 9). Công ty có thể tạo ra bao nhiêu mã số nhân viên theo cách này?
Xem đáp án »
13/07/2024
3,652
Câu 5:
Tung một đồng xu 5 lần liên tiếp và ghi lại kết quả (ví dụ dùng kí hiệu SSNSN để chỉ kết quả 5 lần tung lần lượt là sấp, sấp, ngửa, sấp, ngửa). Có bao nhiêu kết quả khác nhau có thể xảy ra?
Tung một đồng xu 5 lần liên tiếp và ghi lại kết quả (ví dụ dùng kí hiệu SSNSN để chỉ kết quả 5 lần tung lần lượt là sấp, sấp, ngửa, sấp, ngửa). Có bao nhiêu kết quả khác nhau có thể xảy ra?
Xem đáp án »
13/07/2024
2,312
Câu 6:
Mã xác thực (OTP - One Time Password) do một ngân hàng gửi vào điện thoại của khách hàng cho mỗi lần giao dịch là một dãy 6 kí tự từ các chữ số từ 0 đến 9. Có thể tạo ra bao nhiêu mã xác thực khác nhau như vậy?
Xem đáp án »
13/07/2024
1,652
Câu 7:
Một khoá tổ hợp với đĩa quay có 40 vạch số (xem Hình 7). Mật mã của khoá là một dãy gồm 3 số, kí hiệu là a – b – c, mỗi số là một số tự nhiên từ 0 đến 39. Để mở khoá, cần quay mặt số ngược chiều kim đồng hồ cho đến khi điểm mốc gặp vạch số a lần thứ ba, rồi quay mặt số theo chiều ngược lại cho đến khi điểm mốc gặp vạch số b lần thứ hai, cuối cùng quay mặt số ngược chiều kim đồng hồ cho đến khi điểm mốc gặp vạch số c lần đầu tiên. Nếu a, b, c phải khác nhau đôi một, thì có bao nhiêu cách chọn mật mã cho khoá tổ hợp trên?
Một khoá tổ hợp với đĩa quay có 40 vạch số (xem Hình 7). Mật mã của khoá là một dãy gồm 3 số, kí hiệu là a – b – c, mỗi số là một số tự nhiên từ 0 đến 39. Để mở khoá, cần quay mặt số ngược chiều kim đồng hồ cho đến khi điểm mốc gặp vạch số a lần thứ ba, rồi quay mặt số theo chiều ngược lại cho đến khi điểm mốc gặp vạch số b lần thứ hai, cuối cùng quay mặt số ngược chiều kim đồng hồ cho đến khi điểm mốc gặp vạch số c lần đầu tiên. Nếu a, b, c phải khác nhau đôi một, thì có bao nhiêu cách chọn mật mã cho khoá tổ hợp trên?
Xem đáp án »
13/07/2024
1,531
về câu hỏi!