Bài tập Toán 10 Bài tập cuối chương 8 có đáp án
34 người thi tuần này 4.6 0.9 K lượt thi 7 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
20 câu trắc nghiệm Toán 10 Cánh diều Bài tập cuối chương 7 (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 6. Ba đường conic (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 5. Phương trình đường trò (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 4. Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 3. Phương trình đường thẳn (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 2. Biểu thức tọa độ của các phép toán vectơ (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 1. Tọa độ của vectơ (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài ôn tập cuối chương 6 (Đúng sai - trả lời ngắn) có đáp án
Danh sách câu hỏi:
Lời giải
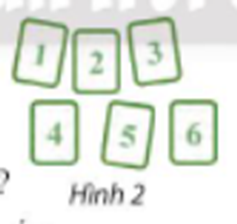
a) Số thành viên của nhóm là 4 + 5 + 6 = 15 (thành viên)
Số cách để nhóm cử ra một thành viên của nhóm tham gia một công việc tình nguyện là tổ hợp chập 1 của 15. Do đó ta có số cách cử một thành viên trong nhóm là:
\(C_{15}^1 = 15\) (cách).
Vậy số cách cử một thành viên trong nhóm là 15 cách.
b) Số cách để nhóm cử ra ba thành viên của nhóm đang học ở ba lớp khác nhau tham gia một công việc tình nguyện là:
\(C_4^1.C_5^1.C_6^1 = 120\)(cách).
Vậy có 120 cách để nhóm cử ra ba thành viên của nhóm đang học ở ba lớp khác nhau tham gia một công việc tình nguyện.
c) Số cách cử ra 2 thành viên của nhóm đang học ở hai lớp khác nhau có thể có 3 phương án khác nhau:
- Phương án 1: 1 thành viên lớp 10A và 1 thành viên lớp 10B, có \(C_4^1.C_5^1 = 20\)(cách).
- Phương án 2: 1 thành viên lớp 10B và 1 thành viên lớp 10C, có \(C_5^1.C_6^1 = 30\)(cách).
- Phương án 3: 1 thành viên lớp 10A và 1 thành viên lớp 10C, có \(C_4^1.C_6^1 = 24\)(cách).
Theo quy tắc cộng, có tất cả 20 + 30 + 24 = 74 cách cử ra 2 thành viên của nhóm đang học ở hai lớp khác nhau tham gia một công việc tình nguyện.
Lời giải
Mật mã là một dãy số có ba chữ số nên việc thiết lập mật mã chia làm ba giai đoạn:
- Chữ số đầu tiên có 10 cách chọn;
- Chữ số thứ hai có 10 cách chọn;
- Chữ số thứ ba có 10 cách chọn.
Theo quy tắc nhân, ta có: 10.10.10 = 1 000 mật mã.
Vậy có tất cả 1 000 cách chọn mật mã cho khóa.
Lời giải
a) Số tự nhiên có sáu chữ số với 6 chữ số được lấy từ 6 thẻ là hoán vị của 6 chữ số. Do đó số số tự nhiên có sáu chữ số là:
P6 = 6! = 6.5.4.3.2.1 = 720 số.
Vậy có tất cả 720 số tự nhiên có sáu chữ số lấy từ các tấm thẻ.
b) Việc lập số tự nhiên lẻ có sáu chữ số lấy từ 6 thẻ được chia làm hai giai đoạn:
- Giai đoạn 1. Chọn chữ số hàng đơn vị lấy từ các tấm thẻ có chữ số lẻ {1; 3; 5}, có 3 cách.
- Giai đoạn 2. Chọn 5 chữ số còn lại lấy từ 5 tấm thẻ còn lại là hoán vị của 5 chữ số, do đó có 5! = 120 cách.
Theo quy tắc nhân, ta có: 3.120 = 360 số tự nhiên lẻ có sáu chữ số.
Vậy có 360 số tự nhiên lẻ có sáu chữ số.
c) Số số tự nhiên có năm chữ số được lấy từ 6 tấm thẻ là chỉnh hợp chập 5 của 6, do đó có \(A_6^5 = 720\) số.
Vậy có 720 số tự nhiên có 5 chữ số được lấy từ 6 tấm thẻ.
d) Gọi số tự nhiên có năm chữ số cần tìm là \(\overline {abcde} \) (trong đó a, b, c, d, e là các số trên tấm thẻ, a ≠ 0).
Vì \(\overline {abcde} > 50000\) nên a có thể bằng 5 hoặc 6, nghĩa là a có 2 cách chọn.
Bốn chữ số còn lại được chọn từ số trên bốn tấm thẻ còn lại là hoán vị của 4 chữ số, do đó có 4! = 24 cách.
Theo quy tắc nhân, ta có: 2.24 = 48 số tự nhiên có năm chữ số lớn hơn 50 000.
Lời giải
Bữa trưa của nhóm khách được chia thành 3 giai đoạn:
- Giai đoạn thứ nhất: Chọn 2 món mặn, có \(C_6^2 = 15\) cách.
- Giai đoạn thứ hai: Ứng với 2 món mặn, chọn 2 món rau có \(C_5^2 = 10\)cách.
- Giai đoạn thứ ba: Ứng với 2 món mặn, 2 món rau, chọn 1 món canh có \(C_3^1 = 3\) cách.
Theo quy tắc nhân, ta có: 15.10.3 = 450 cách.
Vậy nhóm khách có tất cả 450 cách chọn một bữa trưa.
Lời giải
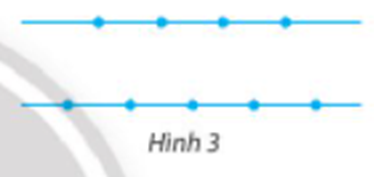
Đặt tên hai đường thẳng song song lần lượt là d, d’ như hình vẽ:
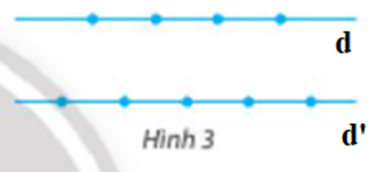
Cách 1: Tam giác có ba đỉnh là ba điểm trong chín điểm đã cho sao cho ba điểm đó không thẳng hàng. Do đó có hai phương án sau:
- Phương án 1: 2 điểm lấy ở đường thẳng d, 1 điểm ở đường thẳng d’, có \(C_4^2.C_5^1 = 30\) cách.
- Phương án 2: 2 điểm lấy ở đường thẳng d’, 1 điểm ở đường thẳng d, có \(C_4^1.C_5^2 = 40\)cách.
Theo quy tắc cộng ta có 30 + 40 = 70 (cách).
Vậy có tất cả 70 tam giác thỏa mãn điều kiện đầu bài.
Cách 2: Tam giác có ba đỉnh là ba điểm trong chín điểm đã cho. Ba điểm được lấy ra phải thỏa mãn ba điểm không cùng nằm trên một đường thẳng. Do đó số tam giác được tạo thành là:
\(C_9^3 - C_4^3 - C_5^3 = 70\)(tam giác).
Vậy có tất cả 70 tam giác thỏa mãn điều kiện đầu bài.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.