Bài tập Toán 10 Bài 1. Dấu của tam thức bậc hai có đáp án

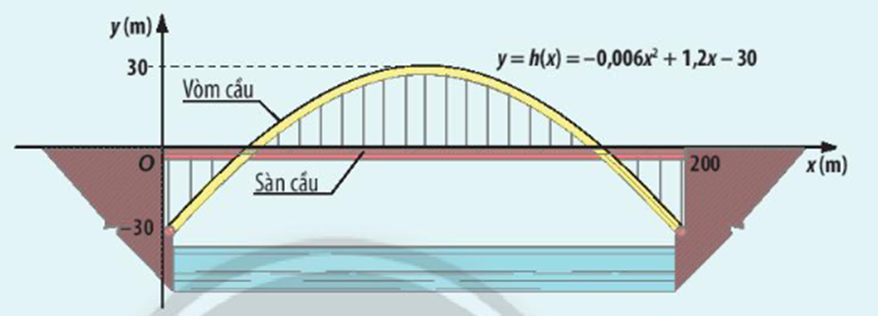
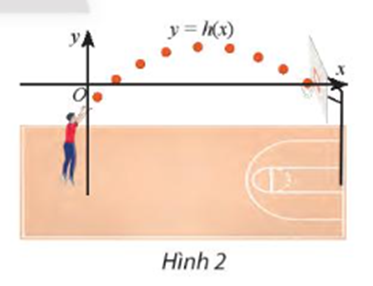
Sau bài học này chúng ta sẽ giải bài toán trên như sau:

Quan sát hình vẽ ta thấy mặt cầu là trục Ox, phần h(x) nằm phía trên mặt cầu nghĩa là h(x) nằm phía trên trục hoành hay là h(x) > 0.

Phần h(x) nằm phía dưới mặt cầu nghĩa là h(x) nằm phía dưới trục hoành hay là h(x) < 0.

Vậy với giá trị của h(x) > 0 thì vòm cầu cao hơn mặt cầu, với giá trị của h(x) < 0 thì vòm cầu thấp hơn mặt cầu.

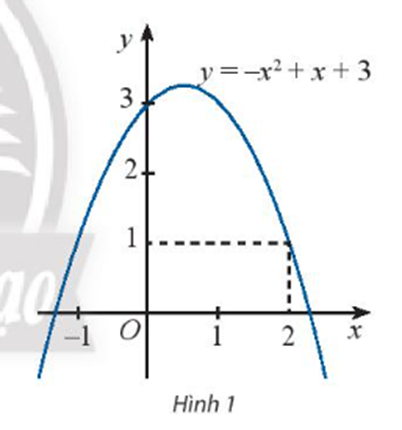
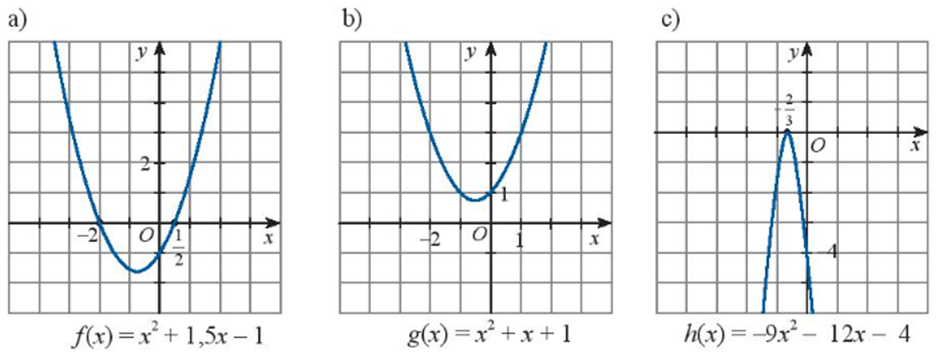
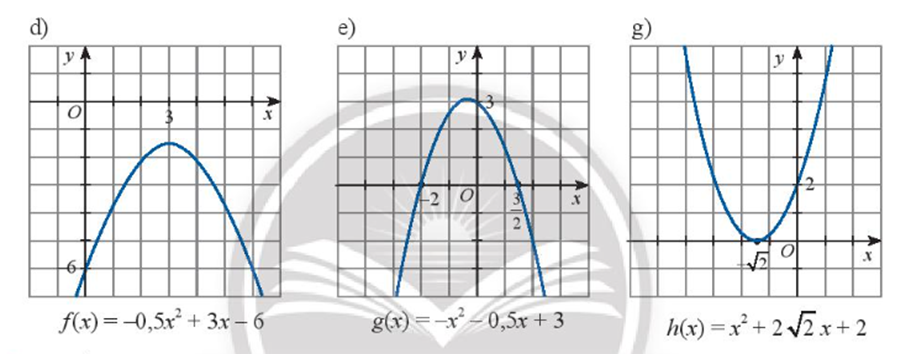
a) Biểu thức f(x) là đa thức bậc 2.

b) Dựa vào đồ thị ta thấy với x = 2 thì f(2) = 1 > 0.

Vậy f(2) mang dấu dương.

a) Biểu thức f(x) = 2x² + x – 1 có dạng tam thức bậc hai với a = 2, b = 1 và c = -1 .

Với x = 1 thì f(1) = 2.1² + 1 – 1 = 2 > 0.

b) Biểu thức g(x) = – x⁴ + 2x² + 1 không có dạng tam thức bậc hai vì bậc của đa thức là bậc 4.

c) Biểu thức h(x) = – x² +$\sqrt{2}$x – 3 có dạng tam thức bậc hai với a = -1, b = $\sqrt{2}$ , c = -3.

a) Tam thức bậc hai f(x) = 2x² – 5x + 2 có ∆ = (-5)² – 4.2.2 = 25 – 16 = 9 > 0. Do đó f(x) có hai nghiệm phân biệt là:

x₁ = $\frac{-\left(-5\right)+\sqrt{9}}{2.2}$ = 2 và x₂ = $\frac{-\left(-5\right)-\sqrt{9}}{2.2}=\frac{1}{2}$.

Vậy biệt thức ∆ = 9 và tam thức có hai nghiệm phân biệt x₁ = 2 và x₂ = .

b) Tam thức bậc hai g(x) = – x² + 6x – 9 có ∆ = 6² – 4.(-1).(-9) = 36 – 36 = 0. Do đó g(x) có nghiệm kép là:

x₁ = x₂ = $\frac{-6+\sqrt{0}}{2.\left(-1\right)}=3$.

Vậy biệt thức ∆ = 0 và tam thức có hai nghiệm kép x = 3.

c) Tam thức bậc hai h(x) = 4x² – 4x + 9 có ∆ = 4² – 4.4.9 = 16 – 144 = - 128 < 0. Do đó f(x) vô nghiệm.

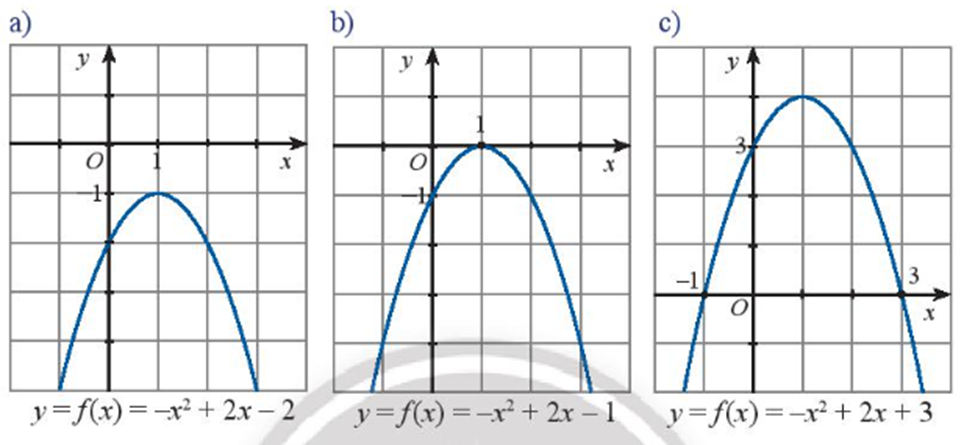
a) Dựa vào hình vẽ ta thấy đồ thị hàm số không cắt trục hoành nên tam thức f(x) = - x² + 2x – 2 vô nghiệm.

Ta có ∆ = 2² – 4(-1).(-2) = 4 – 8 = - 4 < 0.

Tam thức f(x) có hệ số a = -1 < 0.

Ta thấy toàn bộ đồ thị hàm số nằm phía dưới trục hoành nên f(x) < 0 với mọi x.

Suy ra f(x) cùng dấu với hệ số a với mọi x.

b) Dựa vào hình vẽ ta thấy đồ thị hàm số cắt trục hoành tại một điểm duy nhất có hoành độ x = 1 nên tam thức f(x) = - x² + 2x – 1 có một nghiệm duy nhất x = 1.

Ta có ∆ = 2² – 4(-1).(-1) = 4 – 4 = 0.

Tam thức f(x) có hệ số a = -1 < 0.

Ta thấy với x ≠ 1 toàn bộ đồ thị hàm số nằm phía dưới trục hoành nên f(x) < 0 với x ≠ 1 và f(x) = 0 với x = 1.

Suy ra f(x) cùng dấu với hệ số a với x ≠ 1.

c) Dựa vào hình vẽ ta thấy đồ thị hàm số cắt trục hoành tại hai điểm phân biệt có hoành độ lần lượt là x₁ = - 1 và x₂ = 3 nên tam thức f(x) = - x² + 2x + 3 có hai nghiệm phân biệt x₁ = - 1 và x₂ = 3.

Ta có ∆ = 2² – 4.3.(-1) = 4 + 12 = 16 > 0.

Tam thức f(x) có hệ số a = -1 < 0.

Ta thấy với x < - 1 hoặc x > 3 thì đồ thị hàm số nằm phía dưới trục hoành, với -1 < x < 3 thì đồ thị hàm số nằm phía trên trục hoành hay f(x) < 0 với x < -1 hoặc x > 3; f(x) > 0 với -1 < x < 3 và f(x) = 0 tại x = -1 hoặc x = 3.

Suy ra f(x) cùng dấu với hệ số a với x < -1 hoặc x > 3.

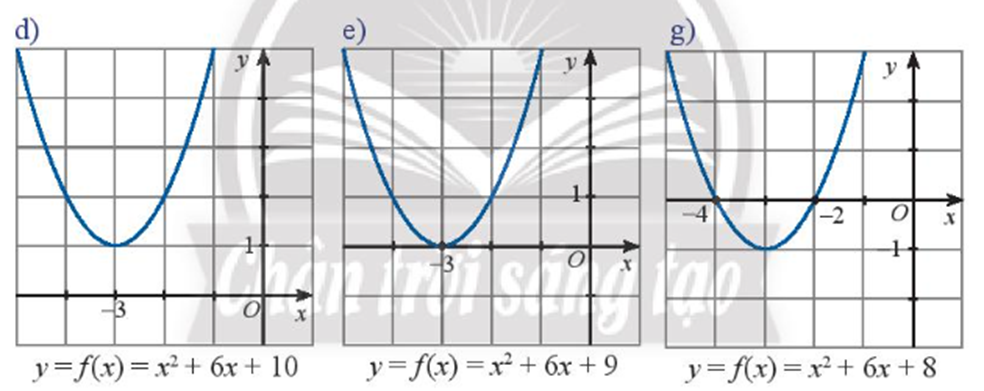
d) Dựa vào hình vẽ ta thấy đồ thị hàm số không cắt trục hoành nên tam thức f(x) = x² + 6x + 10 vô nghiệm.

Ta có ∆ = 6² – 4.1.10 = 36 – 40 = - 4 < 0.

Tam thức f(x) có hệ số a = 1 > 0.

Ta thấy toàn bộ đồ thị hàm số nằm phía trên trục hoành nên f(x) > 0 với mọi x.

Suy ra f(x) cùng dấu với hệ số a với mọi x.

e) Dựa vào hình vẽ ta thấy đồ thị hàm số cắt trục hoành tại một điểm duy nhất có hoành độ x = -3 nên tam thức f(x) = x² + 6x + 9 có một nghiệm duy nhất x = -3.

Ta có ∆ = 6² – 4.1.9 = 36 – 36 = 0.

Tam thức f(x) có hệ số a = 1 > 0.

Ta thấy với x ≠ -3 toàn bộ đồ thị hàm số nằm phía trên trục hoành nên f(x) > 0 với x ≠ - 3 và f(x) = 0 với x = -3.

Suy ra f(x) cùng dấu với hệ số a với x ≠ -3.

g) Dựa vào hình vẽ ta thấy đồ thị hàm số cắt trục hoành tại hai điểm phân biệt có hoành độ lần lượt là x₁ = -4 và x₂ = -2 nên tam thức f(x) = x² + 6x + 8 có hai nghiệm phân biệt x₁ = -4 và x₂ = -2.

Ta có ∆ = 6² – 4.1.8 = 36 – 32 = 4 > 0.

Tam thức f(x) có hệ số a = 1 > 0.

Ta thấy với x < - 4 hoặc x > -2 thì đồ thị hàm số nằm phía trên trục hoành, với -4 < x < -2 thì đồ thị hàm số nằm phía dưới trục hoành hay f(x) > 0 với x < -4 hoặc x > 2; f(x) < 0 với -4 < x < -2 và f(x) = 0 tại x = -4 hoặc x = -2.

Suy ra f(x) cùng dấu với hệ số a với x < -4 hoặc x > -2.