Bài tập Tích của một số với một vectơ có đáp án
37 người thi tuần này 4.6 1.3 K lượt thi 13 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 3
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 2
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 1
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Danh sách câu hỏi:
Lời giải
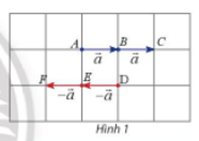
+) Ta có: ;
AC = AB + BC =
Có:
Do đó: .
Vậy vectơ có độ dài là và có cùng hướng với vectơ (theo hướng đi từ trái qua phải).
+) Ta có: ;
DF = DE + EF =
Có:
Do đó: .
Vậy vectơ có độ dài là và ngược hướng với vectơ .
Lời giải
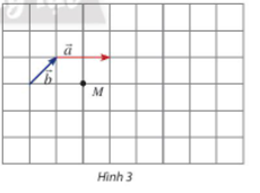
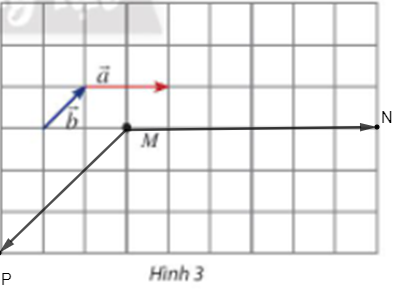
a) Ta có: nên vectơ cùng hướng với vectơ và có độ dài bằng .
Qua M ta vẽ đường thẳng song song với giá của vectơ và lấy điểm N trên đường thẳng đó cùng hướng với vectơ thỏa mãn MN = .
Lại có: nên vectơ ngược hướng với vectơ và có độ dài bằng .
Qua M ta vẽ đường thẳng song song với giá của vectơ và lấy điểm P trên đường thẳng đó ngược hướng với vectơ thỏa mãn .
b) Mỗi ô vuông có cạnh bằng 1 nên đường chéo của mỗi ô vuông có độ dài là .
Ta có vectơ có độ dài là , vectơ có độ dài là .
Ta có: ; .
Lại có: (1).
Ta kí hiệu như hình vẽ dưới với .
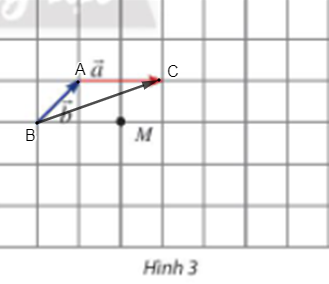
Ta có: (2).
Từ (1) và (2) suy ra: .
Nên .
Ta có:
Áp dụng định lí côsin trong tam giác ABC ta có:
BC2 = AB2 + AC2 – 2 . AB . AC . cosA
= + 22 – 2 . . 2 . cos135° = 10
Suy ra BC = .
Vậy .
Lời giải
+) Giả sử tam giác ABC có trọng tâm G, ta cần chứng minh .
Vì G là trọng tâm của tam giác ABC nên .
Với điểm M bất kì ta có: , , .
Khi đó:
.
Vậy .
+) Giả sử tam giác ABC có 2 điểm M, G thỏa mãn , ta cần chứng minh G là trọng tâm của tam giác ABC.
Ta có:
Vậy G là trọng tâm của tam giác ABC.
Lời giải
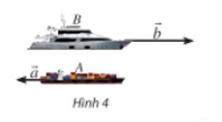
Tàu A đi theo hướng từ đông sau tây, tàu B đi theo hướng từ tây sang đông nên hai tàu đi ngược hướng nhau. Do đó vectơ vận tốc của tàu A là và vectơ vận tốc của tàu B là là hai vectơ ngược hướng.
Ta có: hải lí/giờ, hải lí/giờ.
Suy ra: .
Vì hai vectơ và ngược hướng và .
Do vậy .
Lời giải
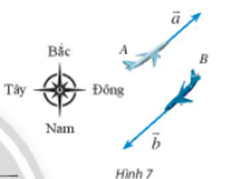
Vì (độ dài của vectơ và khác ).
Nên .
Mà nên vectơ cùng hướng với vectơ .
Do đó vectơ cùng phương với , mà vectơ và cùng phương và khác .
Nên hai vectơ và cùng phương.
Ta lại có: .
Vậy hai vectơ và cùng độ dài và cùng phương.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.