Bài tập Tập hợp có đáp án

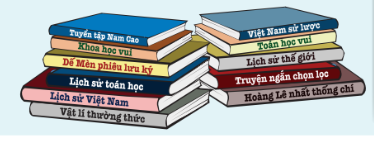
Chúng ta sẽ sắp xếp các cuốn sách thành các nhóm sau:

Nhóm 1 gồm các cuốn sách lịch sử: Việt Nam sử lược, Lịch sử thế giới, Lịch sử Việt Nam.

Nhóm 2 gồm các cuốn sách toán: Lịch sử toán học, Toán học vui.

Nhóm 3 gồm các cuốn sách văn học: Tuyển tập Nam Cao, Dế mèn phiêu lưu kí, Truyện ngắn chọn lọc, Hoàng Lê nhất thống trí.

Nhóm 4 gồm các cuốn sách khoa học: Khoa học vui, Vật lí thưởng thức.

Tương ứng với mỗi nhóm sẽ sắp xếp lên mỗi ngăn của giá sách.

a) Ba ví dụ về tập hợp:

+) A là tập hợp các bạn học sinh trong tổ 1 của lớp 6A.

Các bạn học sinh trong tổ 1 của lớp 6A là: Hoa, Hùng, Dũng, Lê, Mai, Đạt.

Một phần tử thuộc tập hợp A là Hùng.

+) B là tập hợp các môn thể thao yêu thích của lớp 9B.

Các môn thể thao yêu thích của lớp 9B là: Bóng đá, bóng chuyền, cầu Lông, điền kinh.

Một phần tử thuộc tập hợp B là bóng chuyền.

+) C là tập hợp các nước ở khu vực Đông Nam Á.

Các nước trong khu vực Đông Nam Á là: Việt Nam, Lào, Campuchia, Thái Lan, Myanmar, Malaysia, Singapore, Indonesia, Brunei, Philippines và Đông Timor.

Một phần tử thuộc tập hợp C là Việt Nam.

b)

+) Tập hợp $\mathbb{N}$ là tập các số tự nhiên:

Hai phần tử thuộc $\mathbb{N}$ là 1; 15.

Hai phần tử không thuộc $\mathbb{N}$là: -10; 1,2.

+) Tập hợp $\mathbb{Z}$ là tập các số nguyên:

Hai phần tử thuộc $\mathbb{Z}$ là -200; 1 023.

Hai phần tử không thuộc $\mathbb{Z}$là: $\frac{1}{2};$ - 10,25.

+) Tập hợp $\mathbb{Q}$ là tập các số hữu tỉ:

Hai phần tử thuộc $\mathbb{Q}$ là -2,7; 1.

Hai phần tử không thuộc $\mathbb{Q}$là: $\sqrt{2};\pi$.

+) Tập hợp $ℝ$ là tập các số hữu tỉ:

Hai phần tử thuộc $ℝ$ là $-\sqrt{3};\frac{5}{57}$.

Không có phần tử nào không thuộc tập hợp $ℝ$.

a) Các ước của 24 là: -24; -12; -8; -6; -4; -3; -2; -1; 1; 2; 3; 4; 6; 8; 12; 24.

Theo cách liệt kê phần tử, ta có: A = {-24; -12; -8; -6; -4; -3; -2; -1; 1; 2; 3; 4; 6; 8; 12; 24}.

Số phần tử của tập hợp A là 16.

b) Các chữ số xuất hiện trong số 1 113 305 là: 0; 1; 3; 5.

Theo cách liệt kê phần tử, ta có: B = {0; 1; 3; 5}.

Số phần tử của tập hợp B là 4.

c) Tập hợp C là tập hợp gồm các số tự nhiên là bội của 5 và nhỏ hơn hoặc bằng 30.

Ta có bội của 5 là: B(5) = {…; -10; -5; 0; 5; 10; 15; 20; 25; 30; 35; …}

Các bội của 5 là số tự nhiên nhỏ hơn hoặc bằng 30 là: 0; 5; 10; 15; 20; 25; 30.

Theo cách liệt kê phần tử, ta có: C = {0; 5; 10; 15; 20; 25; 30}.

Số phần tử của C là 7.

d) Xét phương trình: x² – 2x + 3 = 0, có:

∆’ = (-1)² – 3 = -2 < 0

Suy ra phương trình vô nghiệm.

Do đó không tồn tại giá trị thực nào của x để x² – 2x + 3 = 0.

⇒ D = $\varnothing$.

Số phần tử của D là 0.

a) Các phần tử của tập hợp A là các số tự nhiên lẻ nhỏ hơn hoặc bằng 15. Khi đó theo cách chỉ ra tính chất đặc trưng, ta viết:

A = {x ∈ $\mathbb{N}$| x là số lẻ và x ≤ 15}.

b) Các phần tử của tập hợp B là các số tự nhiên chia hết cho 5. Khi đó theo cách chỉ ra tính chất đặc trưng, ta viết:

B = {x ∈ $\mathbb{N}$| x chia hết cho 5}.

c) Xét bất phương trình 2x + 5 > 0

⇔ 2x > -5

$\iff x>-\frac{5}{2}$

Khi đó tập hợp C gồm các số thực x thỏa mãn $x>-\frac{5}{2}$.

Ta viết C = $x\in ℝ|x>-\frac{5}{2}$.

a) Tập hợp A có hai phần tử 1 và -1, hai phần tử này cũng thuộc tập hợp B.

Vậy các phần tử của tập của A thuộc tập hợp B.

b) Ta có: $\mathbb{N}$ = {0; 1; 2; 3; 4; …} và $\mathbb{Z}$ = {…; -2; -1; 0; 1; 2; …}.

Các phần tử của tập hợp $\mathbb{N}$ là các số tự nhiên hay cũng là các số 0 và số nguyên dương của tập hợp $\mathbb{Z}$.

Vậy các phần tử của tập hợp A thuộc vào tập hợp B.

c) Các bạn học sinh nữ của lớp chắc chắn thuộc tập hợp các học sinh của lớp đó.

Do đó các phần tử của tập A thuộc vào tập hợp B.