Bài tập Toán 10 Bài 3. Phương trình quy về phương trình bậc hai có đáp án

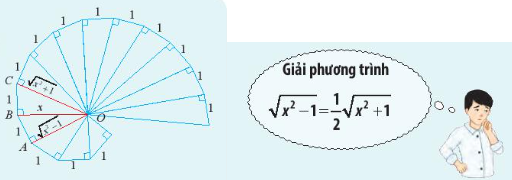
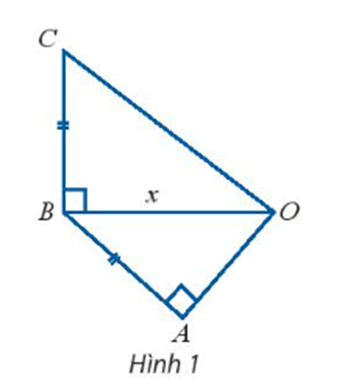
Vì x là độ dài cạnh tam giác vuông nên x > 0.

Ta có OA = \(\frac{1}{2}\)OC

\( \Leftrightarrow \sqrt {{x^2} - 1} = \frac{1}{2}\sqrt {{x^2} + 1} \) (điều kiện x² – 1 ≥ 0 ⇔ x² ≥ 1 \( \Leftrightarrow \left[ \begin{array}{l}x \le - 1\\x \ge 1\end{array} \right.\)).

\( \Leftrightarrow {x^2} - 1 = \frac{1}{4}\left( {{x^2} + 1} \right)\)

⇔ 4x² – 4 = x² + 1

⇔ 3x² = 5

⇔ x² = \(\frac{5}{3}\)

⇔ \(\left[ \begin{array}{l}{x_1} = - \sqrt {\frac{5}{3}} \\{x_2} = \sqrt {\frac{5}{3}} \end{array} \right.\)

Do đó x = \( - \sqrt {\frac{5}{3}} \)(không thỏa mãn) hoặc x = \(\sqrt {\frac{5}{3}} \)(thỏa mãn)

Vậy với x = \(\sqrt {\frac{5}{3}} \) thì OA = \(\frac{1}{2}\)OC.

Lời giải trên sai, vì thiếu bước thử lại nghiệm dẫn đến kết luận nghiệm sai.

Để có lời giải đúng ta làm như sau:

\(\sqrt { - 2{x^2} - 2x + 11} = \sqrt { - {x^2} + 3} \)

⇒ - 2x² – 2x + 11 = -x² + 3 (bình phương cả hai vế làm mất dấu căn)

⇒  x² +2x - 8 = 0               (chuyển vế, rút gọn)

⇒ x = 2 hoặc x = - 4             (giải phương trình bậc hai)

Thay x = 2 vào phương trình đã cho ta được:

Do đó x = 2 không thỏa mãn.

Thay x = -4 vào phương trình đã cho ta được:

\(\sqrt { - 2.{{\left( { - 4} \right)}^2} - 2.\left( { - 4} \right) + 11} = \sqrt { - {{\left( { - 4} \right)}^2} + 3} \Leftrightarrow \sqrt { - 13} = \sqrt { - 13} \) là mệnh đề sai.

Do đó x = -4 không thỏa mãn.

Vậy phương trình đã cho vô nghiệm.

\(\sqrt {31{x^2} - 58x + 1} = \sqrt {10{x^2} - 11x - 19} .\)

⇒ 31x² – 58x + 1 = 10x² – 11x – 19 (bình phương phương trình)

⇒ 21x² – 47x + 20 = 0

⇒ \(\left[ \begin{array}{l}x = \frac{5}{3}\\x = \frac{4}{7}\end{array} \right.\)

Thay lần lượt x = \(\frac{5}{3}\) và x = \(\frac{4}{7}\)vào phương trình đã cho ta thấy không có giá trị nào thỏa mãn.

Vậy phương trình đã cho vô nghiệm.

Lời giải trên sai vì thiếu bước thử lại nghiệm dẫn đến kết luận nghiệm sai.

Lời giải đúng là:

\(\sqrt { - {x^2} + x + 1} = x\)

⇒ - x² + x + 1 = x² (bình phương cả hai vế để làm mất dấu căn)

⇒ - 2x² + x + 1 = 0 (chuyển vế, rút gọn)

⇒ x = 1 hoặc x = \( - \frac{1}{2}\) (giải phương trình bậc hai)

Thay x = 1 và x = \( - \frac{1}{2}\) vào phương trình đã cho ta thấy chỉ có x = 1 là thỏa mãn.

Vậy phương trình đã cho có nghiệm là x = 1.

\(\sqrt {3{x^2} + 27x - 41} = 2x + 3\)

⇒ 3x² + 27x – 41 = 4x² + 12x + 9.

⇒ -x² + 15x – 50 = 0.

⇒ x = 5 hoặc x = 10.

Thay lần lượt x = 5 hoặc x = 10 vào phương trình đã cho ta thấy x = 5 và x = 10 thỏa mãn.

Vậy phương trình đã cho có hai nghiệm x = 5 và x = 10.

Ta có OB = x (cm)

Khi đó AB = BC = x – 1 (cm). Do đó x > 1

Xét tam giác OBC vuông tại B, có:

OC² = OB² + BC² (định lí Py – ta – go)

⇔ OC² = x² + (x – 1)² = 2x² – 2x + 1

⇔ OC = \(\sqrt {2{x^2} - 2x + 1} \)

Xét tam giác OAB vuông tại A, có:

OB² = AB² + OA² (định lí Py – ta – go)

⇔ OA² = OB² – AB²

⇔ OA² = x² – (x – 1)² = x² – (x² – 2x + 1) = 2x – 1

⇔ OA = \(\sqrt {2x - 1} \)

a) Vì OC = 3OA nên \(\sqrt {2{x^2} - 2x + 1} \) = 3\(\sqrt {2x - 1} \)

⇒ 2x² – 2x + 1 = 9(2x – 1)

⇒ 2x² – 2x + 1 = 18x – 9

⇒ 2x² – 20x + 10 = 0

⇒ x² – 10x + 5 = 0

⇒ x = 5 + 2\(\sqrt 5 \) hoặc x = 5 – 2\(\sqrt 5 \).

Thay lần lượt các giá trị trên vào phương trình đã cho, ta thấy cả hai giá trị của x đều là nghiệm của phương trình đã cho. Tuy nhiên x = 5 – 2\(\sqrt 5 \)(không thỏa mãn x > 1)

Vậy với x = 5 + 2\(\sqrt 5 \)(cm) thì OC = 3OA.

b) Vì OC = \(\frac{5}{4}\)OB nên \(\sqrt {2{x^2} - 2x + 1} \) = \(\frac{5}{4}\)x

⇒ 2x² – 2x + 1 = \(\frac{{25}}{{16}}\)x²

⇒ 16(2x² – 2x + 1) = 25x²

⇒ 7x² – 32x + 16 = 0

⇒ x = 4 hoặc x = \(\frac{4}{7}\).

Thay lần lượt các giá trị trên vào phương trình đã cho, ta thấy cả hai giá trị của x đều là nghiệm của phương trình đã cho. Tuy nhiên x = \(\frac{4}{7}\) (không thỏa mãn x > 1)