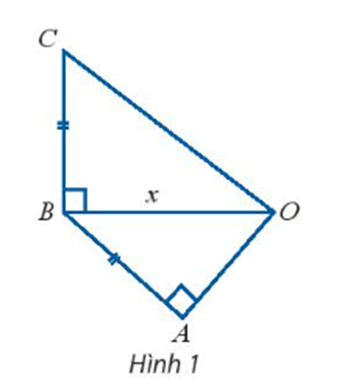
Cho tam giác ABC vuông tại A có AB ngắn hơn AC là 2cm.

a) Biểu diễn độ dài cạnh huyền BC theo AB.

b) Biết chu vi của tam giác ABC là 24 cm. Tìm độ dài ba cạnh của tam giác đó.

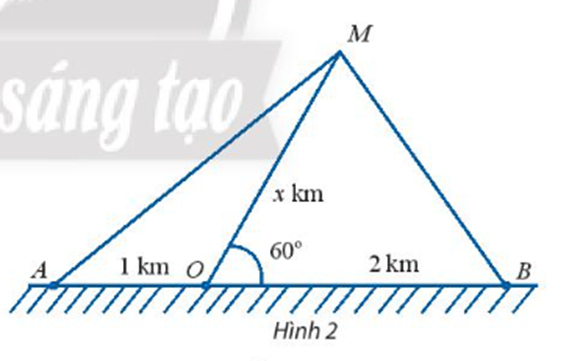
a) Xét tam giác MOB có:

Áp dụng định lí côsin, ta có:

MB² = OM² + OB² – 2.OM.OB.cos\(\widehat {BOM}\)

⇔ MB² = x² + 2² – 2.x.2.cos60°

⇔ MB² = x² + 4 – 2x

⇔ MB = \(\sqrt {{x^2} - 2x + 4} \) (km).

Ta lại có \(\widehat {AOM} + \widehat {BOM} = 180^\circ \) ⇒ \(\widehat {AOM} = 180^\circ - \widehat {BOM} = 180^\circ - 60^\circ = 120^\circ \).

Xét tam giác MOA có:

Áp dụng định lí côsin, ta có:

MA² = OM² + OA² – 2.OM.OA.cos\(\widehat {AOM}\)

⇔ MA² = x² + 1² – 2.x.1.cos120°

⇔ MA² = x² + 1 + x

⇔ MA = \(\sqrt {{x^2} + x + 1} \) (km).

Vậy MA = \(\sqrt {{x^2} + x + 1} \) km và MB = \(\sqrt {{x^2} - 2x + 4} \) km.

b) Để khoảng cách từ tàu đến B bằng \(\frac{4}{5}\) khoảng cách từ tàu đến A thì \(\sqrt {{x^2} - 2x + 4} = \frac{4}{5}\sqrt {{x^2} + x + 1} \)

⇒ x² – 2x + 4 = \(\frac{{16}}{{25}}\)(x² + x + 1)

⇒ 25x² – 50x + 100 = 16x² + 16x + 16

⇒ 9x² – 66x + 84 = 0

⇒ x = \(\frac{{11 - \sqrt {37} }}{3}\) hoặc x = \(\frac{{11 + \sqrt {37} }}{3}\).

Thay lần lượt các giá trị trên vào phương trình đã cho ta thấy cả hai giá trị đều thỏa mãn.

Vậy với x = \(\frac{{11 - \sqrt {37} }}{3}\) hoặc x = \(\frac{{11 + \sqrt {37} }}{3}\) thì khoảng cách từ tàu đến B bằng \(\frac{4}{5}\) khoảng cách từ tàu đến A.

c) Đổi 500 m = 0,5 km = \(\frac{1}{2}\) km

Để khoảng cách từ tàu đến B nhỏ hơn khoảng cách từ tàu đến O 500 m thì

\(\sqrt {{x^2} - 2x + 4} = x - \frac{1}{2}\)

⇔ x² – 2x + 4 = x² – x + \(\frac{1}{4}\)

⇔ – x = \( - \frac{{15}}{4}\).

⇔ x = \(\frac{{15}}{4}\).

Vậy x = \(\frac{{15}}{4}\) thì khoảng cách từ tàu đến B nhỏ hơn khoảng cách từ tàu đến O 500 m.

a) \(\sqrt {11{x^2} - 14x - 12} = \sqrt {3{x^2} + 4x - 7} \)

⇒ 11x² – 14x – 12 = 3x² + 4x – 7

⇒ 8x² – 18x – 5 = 0

⇒ x = \(\frac{5}{2}\) hoặc x = \( - \frac{1}{4}\)

Thay lần lượt các giá trị của x vào phương trình đã cho ta thấy chỉ có x = \(\frac{5}{2}\) là thỏa mãn.

Vậy tập nghiệm của phương trình S = \(\left\{ {\frac{5}{2}} \right\}\).

b) \(\sqrt {{x^2} + x - 42} = \sqrt {2x - 30} \)

⇒ x² + x – 42 = 2x – 30

⇒ x² – x – 12 = 0

⇒ x = - 3 hoặc x = 4

Thay lần lượt x = -3 và x = 4 vào phương trình đã cho ta thấy không có giá trị nào thỏa mãn.

Vậy tập nghiệm của phương trình S = \(\emptyset \).

c) \(2\sqrt {{x^2} - x - 1} = \sqrt {{x^2} + 2x + 5} \)

⇒ 4x² – 4x – 4 = x² + 2x + 5

⇒ 3x² – 6x – 9 = 0

⇒ x = -1 hoặc x = 3

Thay lần lượt các giá trị này vào phương trình đã cho ta thấy x = -1 hoặc x = 3 đều thỏa mãn.

Vậy nghiệm của phương trình là x = -1 và x = 3.

d) \(3\sqrt {{x^2} + x - 1} - \sqrt {7{x^2} + 2x - 5} = 0\)

⇔ \(3\sqrt {{x^2} + x - 1} = \sqrt {7{x^2} + 2x - 5} \)

⇒ 9(x² + x – 1) = 7x² + 2x – 5

⇒ 9x² + 9x – 9 = 7x² + 2x – 5

⇒ 2x² + 7x – 4 = 0.

⇒ x = -4 và x = \(\frac{1}{2}\).

Thay lần lượt hai giá trị này vào phương trình đã cho ta thấy chỉ có x = -4 thỏa mãn.

Vậy nghiệm của phương trình là x = -4.