Câu hỏi:
13/07/2024 6,661
Giải phương trình sau:
a) \(\sqrt {{x^2} + 3x + 1} = 3;\)
b) \(\sqrt {{x^2} - x - 4} = x + 2;\)
c) 2 + \(\sqrt {12 - 2x} \) = x;
d) \(\sqrt {2{x^2} - 3x - 10} = - 5.\)
Giải phương trình sau:
a) \(\sqrt {{x^2} + 3x + 1} = 3;\)
b) \(\sqrt {{x^2} - x - 4} = x + 2;\)
c) 2 + \(\sqrt {12 - 2x} \) = x;
d) \(\sqrt {2{x^2} - 3x - 10} = - 5.\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) \(\sqrt {{x^2} + 3x + 1} = 3\)
⇒ x2 + 3x + 1 = 9
⇒ x2 + 3x – 8 = 0
⇒ x = \(\frac{{ - 3 - \sqrt {41} }}{2}\) hoặc x = \(\frac{{ - 3 + \sqrt {41} }}{2}\).
Thay lần lượt hai giá trị này vào phương trình đã cho ta thấy cả hai giá trị đều thỏa mãn.
Vậy phương trình đã cho có tập nghiệm \(S = \left\{ {\frac{{ - 3 - \sqrt {41} }}{2};\frac{{ - 3 + \sqrt {41} }}{2}} \right\}\).
b) \(\sqrt {{x^2} - x - 4} = x + 2\)
⇒ x2 – x – 4 = x2 + 4x + 4
⇒ – 5x = 8
⇒ x = \( - \frac{8}{5}\)
Thay x = \( - \frac{8}{5}\) vào phương trình đã cho ta thấy thỏa mãn.
Vậy nghiệm của phương trình đã cho là x = \( - \frac{8}{5}\).
c) 2 + \(\sqrt {12 - 2x} \) = x
⇔ \(\sqrt {12 - 2x} \)= x – 2
⇒ 12 – 2x = x2 – 4x + 4
⇒ x2 – 2x – 8 = 0
⇒ x = 4 hoặc x = - 2
Thay lần lượt từng giá trị của x vào phương trình đã cho ta thấy chỉ có x = 4 thỏa mãn.
Vậy nghiệm của phương trình đã cho là x = 4.
d) \(\sqrt {2{x^2} - 3x - 10} = - 5.\)
⇒ 2x2 – 3x – 10 = 25
⇒ 2x2 – 3x – 35 = 0
⇒ x = 5 và x = \( - \frac{7}{2}\)
Thay lần lượt từng giá trị của x vào phương trình đã cho ta thấy không có giá trị nào thỏa mãn.
Vậy phương trình đã cho vô nghiệm.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
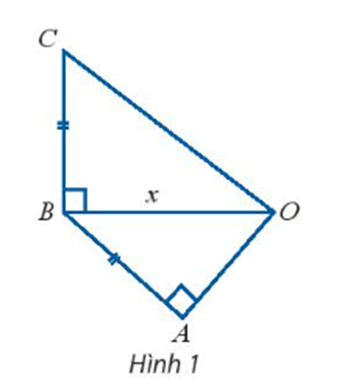
a) Xét tam giác MOB có:
Áp dụng định lí côsin, ta có:
MB2 = OM2 + OB2 – 2.OM.OB.cos\(\widehat {BOM}\)
⇔ MB2 = x2 + 22 – 2.x.2.cos60°
⇔ MB2 = x2 + 4 – 2x
⇔ MB = \(\sqrt {{x^2} - 2x + 4} \) (km).
Ta lại có \(\widehat {AOM} + \widehat {BOM} = 180^\circ \) ⇒ \(\widehat {AOM} = 180^\circ - \widehat {BOM} = 180^\circ - 60^\circ = 120^\circ \).
Xét tam giác MOA có:
Áp dụng định lí côsin, ta có:
MA2 = OM2 + OA2 – 2.OM.OA.cos\(\widehat {AOM}\)
⇔ MA2 = x2 + 12 – 2.x.1.cos120°
⇔ MA2 = x2 + 1 + x
⇔ MA = \(\sqrt {{x^2} + x + 1} \) (km).
Vậy MA = \(\sqrt {{x^2} + x + 1} \) km và MB = \(\sqrt {{x^2} - 2x + 4} \) km.
b) Để khoảng cách từ tàu đến B bằng \(\frac{4}{5}\) khoảng cách từ tàu đến A thì \(\sqrt {{x^2} - 2x + 4} = \frac{4}{5}\sqrt {{x^2} + x + 1} \)
⇒ x2 – 2x + 4 = \(\frac{{16}}{{25}}\)(x2 + x + 1)
⇒ 25x2 – 50x + 100 = 16x2 + 16x + 16
⇒ 9x2 – 66x + 84 = 0
⇒ x = \(\frac{{11 - \sqrt {37} }}{3}\) hoặc x = \(\frac{{11 + \sqrt {37} }}{3}\).
Thay lần lượt các giá trị trên vào phương trình đã cho ta thấy cả hai giá trị đều thỏa mãn.
Vậy với x = \(\frac{{11 - \sqrt {37} }}{3}\) hoặc x = \(\frac{{11 + \sqrt {37} }}{3}\) thì khoảng cách từ tàu đến B bằng \(\frac{4}{5}\) khoảng cách từ tàu đến A.
c) Đổi 500 m = 0,5 km = \(\frac{1}{2}\) km
Để khoảng cách từ tàu đến B nhỏ hơn khoảng cách từ tàu đến O 500 m thì
\(\sqrt {{x^2} - 2x + 4} = x - \frac{1}{2}\)
⇔ x2 – 2x + 4 = x2 – x + \(\frac{1}{4}\)
⇔ – x = \( - \frac{{15}}{4}\).
⇔ x = \(\frac{{15}}{4}\).
Vậy x = \(\frac{{15}}{4}\) thì khoảng cách từ tàu đến B nhỏ hơn khoảng cách từ tàu đến O 500 m.
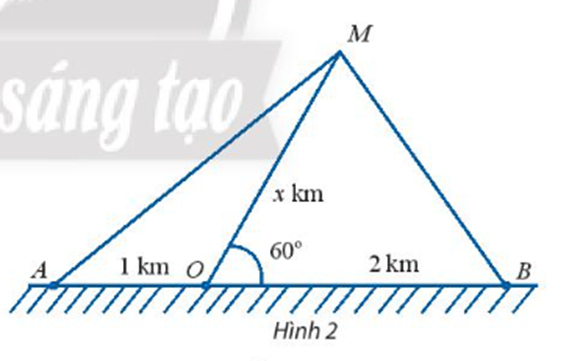
Lời giải
Gọi AB = x (cm) (x > 0)
Vì AB ngắn hơn AC là 2cm nên AC = x + 2 (cm).
a) Xét tam giác ABC vuông tại A, có:
BC2 = AB2 + AC2 (định lí Py – ta – go)
⇔ BC2 = x2 + (x + 2)2
⇔ BC2 = x2 + x2 + 4x + 4
⇔ BC2 = 2x2 + 4x + 4
⇔ BC = \(\sqrt {2{x^2} + 4x + 4} \) (cm)
Vậy BC = \(\sqrt {2{x^2} + 4x + 4} \) (cm).
b) Chu vi của tam giác ABC là:
AB + AC + BC = x + x + 2 + \(\sqrt {2{x^2} + 4x + 4} \) = 2x + 2 + \(\sqrt {2{x^2} + 4x + 4} \) (cm).
Mà chu vi của tam giác ABC là 24cm nên ta có phương trình:
2x + 2 + \(\sqrt {2{x^2} + 4x + 4} \) = 24
⇔ \(\sqrt {2{x^2} + 4x + 4} \) = 22 – 2x
⇒ 2x2 + 4x + 4 = 484 – 88x + 4x2
⇒ 2x2 – 92x + 480 = 0
⇒ x2 – 46x + 240 = 0
⇒ x = 40 và x = 6.
Thay lần lượt hai nghiệm vào phương trình đã cho ta thấy x = 6 thỏa mãn.
Với x = 6 thì AB = 6 cm, AC = 6 + 2 = 8 cm, BC = \(\sqrt {{{2.6}^2} + 4.6 + 4} = 10\) cm.
Vậy độ dài các cạnh của tam giác ABC lần lượt là AB = 6cm, AC = 8cm, BC = 10 cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
13 câu Trắc nghiệm Tích của vectơ với một số có đáp án (Thông hiểu)
-
12 Bài tập Ứng dụng của hàm số bậc hai để giải bài toán thực tế (có lời giải)
-
10 Bài tập Ứng dụng ba đường conic vào các bài toán thực tế (có lời giải)
-
Bộ 2 Đề kiểm tra giữa học kì 2 Toán 10 Kết nối tri thức có đáp án - Đề 1
-
16 câu Trắc nghiệm Toán 10 Kết nối tri thức Mệnh đề có đáp án
-
10 Bài tập Tính số trung bình, trung vị, tứ phân vị và mốt của mẫu số liệu cho trước (có lời giải)
-
185 câu Trắc nghiệm Toán 10 Bài 1:Phương trình đường thẳng trong mặt phẳng oxy có đáp án (Mới nhất)
-
50 câu trắc nghiệm Thống kê cơ bản (phần 1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận