Bài tập Toán 10 Bài tập cuối chương 7 có đáp án

a) Tam thức bậc hai f(x) = 6x² + 41x + 44 có ∆ = 41² – 4.6.44 = 625 > 0 và a = 6 > 0. Do đó f(x) có hai nghiệm phân biệt x₁ = \( - \frac{4}{3}\) và x₂ = \( - \frac{{11}}{2}\).

Khi đó ta có bảng xét dấu sau:

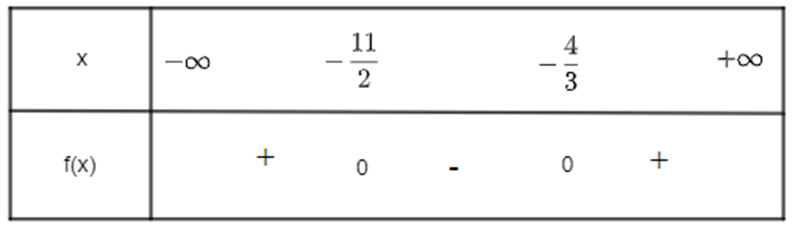
Vậy f(x) âm khi x thuộc khoảng \(\left( { - \frac{{11}}{2}; - \frac{4}{3}} \right)\), f(x) dương khi x thuộc hai khoảng \(\left( { - \infty ; - \frac{{11}}{2}} \right)\) và \(\left( { - \frac{4}{3}; + \infty } \right)\).

b) Tam thức bậc hai g(x) = - 3x² + x – 1 có ∆ = 1² – 4.(-3).(-1) = -11 < 0 và a = -3 < 0. Do đó g(x) vô nghiệm. Khi đó ta có bảng xét dấu sau: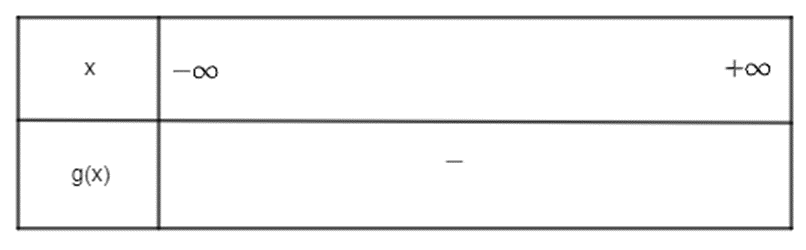

Vậy g(x) âm với mọi x ∈ ℝ.

c) Tam thức bậc hai h(x) = 9x² + 12x + 4 có ∆ = 12² – 4.9.4 = 0 và a = 9 > 0. Do đó h(x) có nghiệm kép x₁ = x₂ = \(\frac{{ - 2}}{3}\).

Khi đó ta có bảng xét dấu sau:

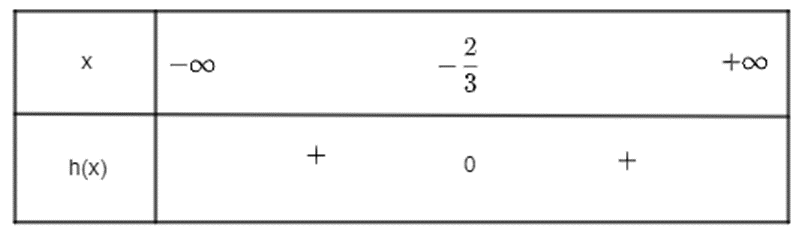
Vậy h(x) dương với mọi x ≠ \(\frac{{ - 2}}{3}\).

a) Tam thức bậc hai f(x) = 7x² – 19x – 6 có a = 7 > 0 và ∆ = 19² – 4.7.(-6) = 529 > 0. Do đó f(x) có hai nghiệm phân biệt x₁ = 3 và x₂ = \( - \frac{2}{7}\).

Suy ra f(x) dương khi x thuộc khoảng \(\left( { - \infty ; - \frac{2}{7}} \right)\) và (3; +∞), f(x) âm khi x thuộc khoảng \(\left( { - \frac{2}{7};3} \right)\) và f(x) = 0 khi x = 3 và x = \( - \frac{2}{7}\).

Vậy bất phương trình đã cho có tập nghiệm là S = \(\left( { - \infty ; - \frac{2}{7}} \right]\) ∪ [3; +∞).

b) Tam thức bậc hai g(x) = – 6x² + 11x – 10 có a = - 6 < 0 và ∆ = 11² – 4.(-6).(-10) = -119 < 0. Do đó g(x) vô nghiệm.

Suy ra g(x) luôn âm với mọi x thuộc ℝ

Vậy bất phương trình đã cho có tập nghiệm là S = \(\emptyset \).

c) Ta có: 3x² – 4x + 7 > x² + 2x + 1

⇔ 2x² – 6x + 6 > 0

Tam thức bậc hai h(x) = 2x² – 6x + 6 có a = 2 > 0 và ∆’ = 3² – 2.6 = - 3 < 0. Do đó h(x) có vô nghiệm.

Suy ra h(x) dương với mọi x thuộc ℝ.

Vậy bất phương trình đã cho có tập nghiệm S = ℝ.

d) Ta có tam thức bậc hai k(x) = x² – 10x + 25 có a = 1 > 0 và ∆’ = 5² – 25 = 0. Do đó k(x) có nghiệm kép x₁ = x₂ = 5.

Suy ra f(x) dương khi x ≠ 5 và f(x) = 0 khi x = 5.

Vậy bất phương trình đã cho có tập nghiệm là S = {5}.

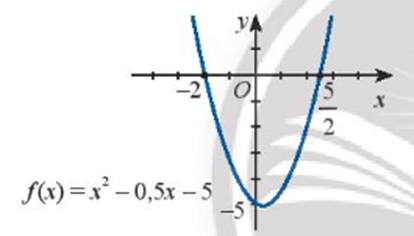
a) Quan sát đồ thị ta thấy:

Với x thuộc hai khoảng (-∞; -2) và \(\left( {\frac{5}{2}; + \infty } \right)\) thì đồ thị hàm số nằm phía trên trục hoành. Do đó f(x) > 0 khi x ∈ (-∞; -2) ∪ \(\left( {\frac{5}{2}; + \infty } \right)\) .

Với x thuộc \(\left( { - 2;\frac{5}{2}} \right)\) thì đồ thị hàm số nằm phía dưới trục hoành. Do đó f(x) < 0 khi x ∈ \(\left( { - 2;\frac{5}{2}} \right)\).

Đồ thị hàm số cắt trục hoành tại hai điểm có hoành độ x = - 2 và x = \(\frac{5}{2}\).

Vậy bất phương trình có tập nghiệm là S = \(\left[ { - 2;\frac{5}{2}} \right]\).

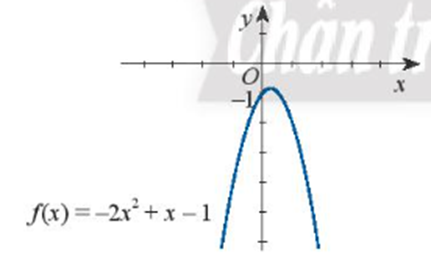
b) Quan sát hình vẽ ta thấy:

Đồ thị hàm số nằm hoàn toàn phía dưới trục hoành với mọi giá trị của x. Do đó f(x) < 0 với mọi x.

Vậy bất phương trình đã cho vô nghiệm.

a) \(\sqrt {{x^2} - 7x} = \sqrt { - 9{x^2} - 8x + 3} \)

⇒ x² – 7x = - 9x² – 8x + 3

⇒ 10x² + x – 3 = 0

⇒ x = \(\frac{1}{2}\) và x = \( - \frac{3}{5}\)

Thay lần lượt hai giá trị vào phương trình đã cho ta thấy chỉ có giá trị x = \( - \frac{3}{5}\) thỏa mãn.

Vậy tập nghiệm của phương trình đã cho là S = \(\left\{ { - \frac{3}{5}} \right\}\).

b) \(\sqrt {{x^2} + x + 8} - \sqrt {{x^2} + 4x + 1} = 0\)

⇒ \(\sqrt {{x^2} + x + 8} = \sqrt {{x^2} + 4x + 1} \)

⇒ x² + x + 8 = x² + 4x + 1

⇒ 3x = 7

⇒ x = \(\frac{7}{3}\)

Thay x = \(\frac{7}{3}\) vào phương trình đã cho ta thấy thỏa mãn.

Vậy tập nghiệm của phương trình là S = \(\left\{ {\frac{7}{3}} \right\}\).

c) \(\sqrt {4{x^2} + x - 1} = x + 1\)

⇒ 4x² + x – 1 = x² + 2x + 1

⇒ 3x² – x – 2 = 0

⇒ x = 1 và x = \( - \frac{2}{3}\)

Thay lần lượt các giá trị của x vào phương trình đã cho ta thấy cả hai giá trị đều thỏa mãn.

Vậy tập nghiệm của phương trình là S = \(\left\{ { - \frac{2}{3};1} \right\}\).

d) \(\sqrt {2{x^2} - 10x - 29} = \sqrt {x - 8} \)

⇒ 2x² – 10x – 29 = x – 8

⇒ 2x² – 11x – 21 = 0

⇒ x = 7 và x = \( - \frac{3}{2}\)

Thay lần lượt hai giá trị này vào phương trình đã cho ta thấy cả hai giá trị đều không thỏa mãn.

Không mất tính tổng quát giả sử tam giác cần xét là tam giác vuông tại A có độ dài cạnh AC ngắn hơn cạnh huyền BC 8cm.

Đặt BC = x (cm)

Khi đó AC = x – 8 (cm)

Xét tam giác ABC vuông tại A, có:

BC² = AB² + AC² (định lí Py – ta – go)

⇔ x² = AB² + (x – 8)²

⇔ AB² = x² – (x – 8)²

⇔ AB² = x² – (x² – 16x + 64)

⇔ AB² = 16x – 64

⇔ AB = \(\sqrt {16x - 64} \) (cm)

Chu vi tam giác ABC là: x + x – 8 + \(\sqrt {16x - 64} \) = 2x – 8 + \(\sqrt {16x - 64} \) (cm)

Mà chu vi tam giác bằng 30cm nên có phương trình 2x – 8 + \(\sqrt {16x - 64} \)= 30

⇒ \(\sqrt {16x - 64} \)= 38 – 2x

⇒ 16x – 64 = 1 444 – 152x + 4x²

⇒ 4x² – 168x + 1 508 = 0

⇒ x² – 42x + 377 = 0

⇒ x = 29 và x = 13

Thay lần lượt vào phương trình đã cho ta thấy chỉ có x = 13 thỏa mãn.

Vậy độ dài cạnh huyền bằng 13cm thì tam giác thỏa mãn điều kiện đầu bài.

Quả bóng nằm ở độ cao trên 40m nghĩa là h(t) > 40 hay - 4,9t² + 30t + 2 > 40

⇔ - 4,9t² + 30t – 38 > 0

Tam thức bậc hai f(t) = - 4,9t² + 30t – 38, có a = -4,9 < 0 và ∆’ = 15² – (-4,9).(-38) = \(\frac{{194}}{5}\) > 0. Do đó f(t) có hai nghiệm phân biệt t₁ ≈ 4,3 và t₂ ≈ 1,8.

Khi đó ta có bảng xét dấu: