Lợi nhuận một tháng p(x) của một quán ăn phụ thuộc vào giá trung bình x của các món ăn theo công thức p(x) = -30x2 + 2 100x – 15 000, với đơn vị tính bằng nghìn đồng. Nếu muốn lợi nhuận trung bình kh...

Ta có 15 triệu = 15 000 (nghìn đồng) Lợi nhuận trung bình không dưới 15 triệu nghĩa là p(x) = -30x2 + 2 100x – 15 000 ≥ 15 000 ⇔ -30x2 + 2 100x – 30 000 ≥ 0 ⇔ -x2 + 70x – 1 000 ≥ 0 Tam thức bậc hai f(x) = -x2 + 70x – 1 000 có a = -1 < 0 và ∆ = 702 – 4.(-1).(-1 000) = 900 > 0. Do đó f(x) có hai nghiệm phân biệt x1 = 50 và x2 = 20. Suy ra f(x) dương khi x thuộc khoảng (20; 50). Do đó bất phương trình f(x) ≥ 0 với x thuộc [20; 50]. Vậy để lợi nhuận trung bình không dưới 15 triệu một tháng thì giá bán trung bình của các món ăn cần có giá từ 20 nghìn đồng đến 50 nghìn đồng.

Câu hỏi:

13/07/2024 13,981

Lợi nhuận một tháng p(x) của một quán ăn phụ thuộc vào giá trung bình x của các món ăn theo công thức p(x) = -30x² + 2 100x – 15 000, với đơn vị tính bằng nghìn đồng. Nếu muốn lợi nhuận trung bình không dưới 15 triệu một tháng thì giá bán trung bình của các món ăn cần nằm trong khoảng nào?

Xem lời giải

Câu hỏi trong đề: Bài tập Toán 10 Bài tập cuối chương 7 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Ta có 15 triệu = 15 000 (nghìn đồng)

Lợi nhuận trung bình không dưới 15 triệu nghĩa là p(x) = -30x² + 2 100x – 15 000 ≥ 15 000

⇔ -30x² + 2 100x – 30 000 ≥ 0

⇔ -x² + 70x – 1 000 ≥ 0

Tam thức bậc hai f(x) = -x² + 70x – 1 000 có a = -1 < 0 và ∆ = 70² – 4.(-1).(-1 000) = 900 > 0. Do đó f(x) có hai nghiệm phân biệt x₁ = 50 và x₂ = 20.

Suy ra f(x) dương khi x thuộc khoảng (20; 50).

Do đó bất phương trình f(x) ≥ 0 với x thuộc [20; 50].

Vậy để lợi nhuận trung bình không dưới 15 triệu một tháng thì giá bán trung bình của các món ăn cần có giá từ 20 nghìn đồng đến 50 nghìn đồng.

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một chú cá heo nhảy lên khỏi mặt nước. Độ cao h(mét) của cá heo với mặt nước sau t giây được cho bởi hàm số:

h(t) = - 4,9t² + 9,6t

Tính khoảng thời gian cá heo ở trên không.

Xem đáp án

Lời giải

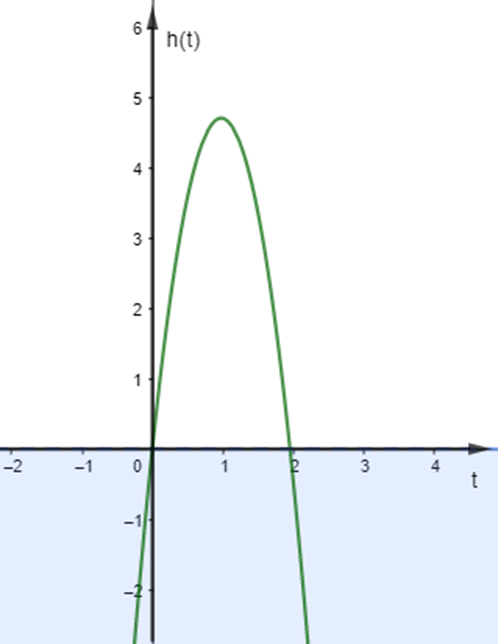
Một chú cá heo nhảy lên khỏi mặt nước. Độ cao h(mét) của cá heo với mặt nước sau (ảnh 1)

Đặt hệ trục tọa độ như hình vẽ với Ot biểu diễn thời gian (giây) là trục trùng với mặt nước, trục h(t) biểu diễn độ cao (mét), độ cao h(t) = - 4,9t² + 9,6t là hàm bậc hai được biểu diễn bởi đường cong parabol màu xanh trên hình vẽ.

Khoảng thời gian cá heo ở trên không tính từ khi cá heo rời khỏi mặt nước nên chính là phần đồ thị nằm trên trục Ot hay - 4,9t² + 9,6t > 0.

Tam thức bậc hai h(t) = - 4,9t² + 9,6t có a = -4,9 < 0 và ∆ = 9,6² – 4.(-4,9).0 = 92,16 > 0. Do đó h(t) có hai nghiệm phân biệt t₁ = 0 và t₂ = $\frac{{96}}{{49}}$.

Suy ra h(t) dương khi t thuộc khoảng $\left( {0;\frac{{96}}{{49}}} \right)$.

Do đó h(t) > 0 khi t ∈ $\left( {0;\frac{{96}}{{49}}} \right)$.

Vậy khoảng thời gian cá heo ở trên không là $\frac{96}{49}$ giây.

Câu 2

Một tam giác vuông có một cạnh góc vuông ngắn hơn cạnh huyền 8cm. Tính độ dài cạnh huyền, biết chu vi tam giác 30 cm.

Xem đáp án

Lời giải

Không mất tính tổng quát giả sử tam giác cần xét là tam giác vuông tại A có độ dài cạnh AC ngắn hơn cạnh huyền BC 8cm.

Đặt BC = x (cm)

Khi đó AC = x – 8 (cm)

Xét tam giác ABC vuông tại A, có:

BC² = AB² + AC² (định lí Py – ta – go)

⇔ x² = AB² + (x – 8)²

⇔ AB² = x² – (x – 8)²

⇔ AB² = x² – (x² – 16x + 64)

⇔ AB² = 16x – 64

⇔ AB = $\sqrt {16x - 64} $ (cm)

Chu vi tam giác ABC là: x + x – 8 + $\sqrt {16x - 64} $ = 2x – 8 + $\sqrt {16x - 64} $ (cm)

Mà chu vi tam giác bằng 30cm nên có phương trình 2x – 8 + $\sqrt {16x - 64} $= 30

⇒ $\sqrt {16x - 64} $= 38 – 2x

⇒ 16x – 64 = 1 444 – 152x + 4x²

⇒ 4x² – 168x + 1 508 = 0

⇒ x² – 42x + 377 = 0

⇒ x = 29 và x = 13

Thay lần lượt vào phương trình đã cho ta thấy chỉ có x = 13 thỏa mãn.

Vậy độ dài cạnh huyền bằng 13cm thì tam giác thỏa mãn điều kiện đầu bài.

Câu 3

Một quả bóng được bắn thẳng lên độ cao 2m với vận tốc ban đầu là 30m/s. Khoảng cách của quả bóng sau t giây được cho bởi hàm số

h(t) = - 4,9t² + 30t + 2,

với h(t) tính bằng đơn vị mét. Hỏi quả bóng nằm ở độ cao trên 40m trong bao nhiêu lâu? Làm tròn kết quả đến hàng phần mười.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Giải các phương trình sau:

a) $\sqrt {{x^2} - 7x} = \sqrt { - 9{x^2} - 8x + 3} $;

b) $\sqrt {{x^2} + x + 8} - \sqrt {{x^2} + 4x + 1} = 0$;

c) $\sqrt {4{x^2} + x - 1} = x + 1$;

d) $\sqrt {2{x^2} - 10x - 29} = \sqrt {x - 8} $.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Giải các bất phương trình sau:

a) 7x² – 19x – 6 ≥ 0;

b) – 6x² + 11x > 10;

c) 3x² – 4x + 7 > x² + 2x + 1;

d) x² – 10x + 25 ≤ 0.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Xét dấu của các tam thức bậc hai sau:

a) f(x) = 6x² + 41x + 44;

b) g(x) = - 3x² + x – 1;

c) h(x) = 9x² + 12x + 4.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Một chú cá heo nhảy lên khỏi mặt nước. Độ cao h(mét) của cá heo với mặt nước sau t giây được cho bởi hàm số:

h(t) = - 4,9t² + 9,6t

Tính khoảng thời gian cá heo ở trên không.

Một tam giác vuông có một cạnh góc vuông ngắn hơn cạnh huyền 8cm. Tính độ dài cạnh huyền, biết chu vi tam giác 30 cm.

Giải các phương trình sau:

a) \(\sqrt {{x^2} - 7x} = \sqrt { - 9{x^2} - 8x + 3} \);

b) \(\sqrt {{x^2} + x + 8} - \sqrt {{x^2} + 4x + 1} = 0\);

c) \(\sqrt {4{x^2} + x - 1} = x + 1\);

d) \(\sqrt {2{x^2} - 10x - 29} = \sqrt {x - 8} \).

Giải các bất phương trình sau:

a) 7x² – 19x – 6 ≥ 0;

b) – 6x² + 11x > 10;

c) 3x² – 4x + 7 > x² + 2x + 1;

d) x² – 10x + 25 ≤ 0.

Xét dấu của các tam thức bậc hai sau:

a) f(x) = 6x² + 41x + 44;

b) g(x) = - 3x² + x – 1;

c) h(x) = 9x² + 12x + 4.