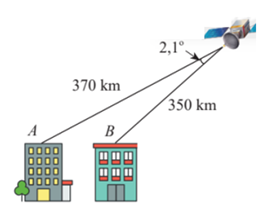
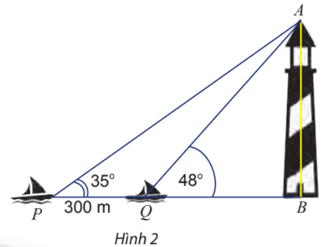
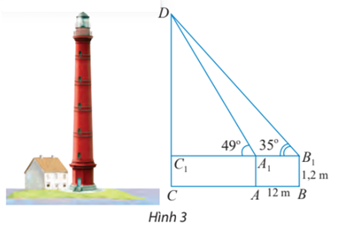
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
20 câu trắc nghiệm Toán 10 Cánh diều Bài tập cuối chương 7 (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 6. Ba đường conic (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 5. Phương trình đường trò (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 4. Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 3. Phương trình đường thẳn (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 2. Biểu thức tọa độ của các phép toán vectơ (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 1. Tọa độ của vectơ (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài ôn tập cuối chương 6 (Đúng sai - trả lời ngắn) có đáp án
Danh sách câu hỏi:
Lời giải
Áp dụng định lí côsin ta có:
c2 = a2 + b2 – 2abcosC = 49,42 + 26,42 – 2.49,4.26,4.cos47°20' ≈ 1 369,6
⇒ c = .
Áp dụng hệ quả của định lí côsin ta có
cosA = .
⇒ .
Tam giác ABC có:
Vậy ; ; c ≈ 37.
Lời giải
Áp dụng hệ quả của định lí côsin ta có:
cosA =
⇒
cosB =
⇒
Tam giác ABC có:
Vậy ; ; .
Lời giải
a) Áp dụng hệ quả của định lí côsin ta có:
cosC =
⇒
Suy ra
Vậy tam giác ABC là tam giác tù.
b) Do AM là đường trung tuyến nên M là trung điểm của BC, tức là MB = MC = BC : 2 = 4.
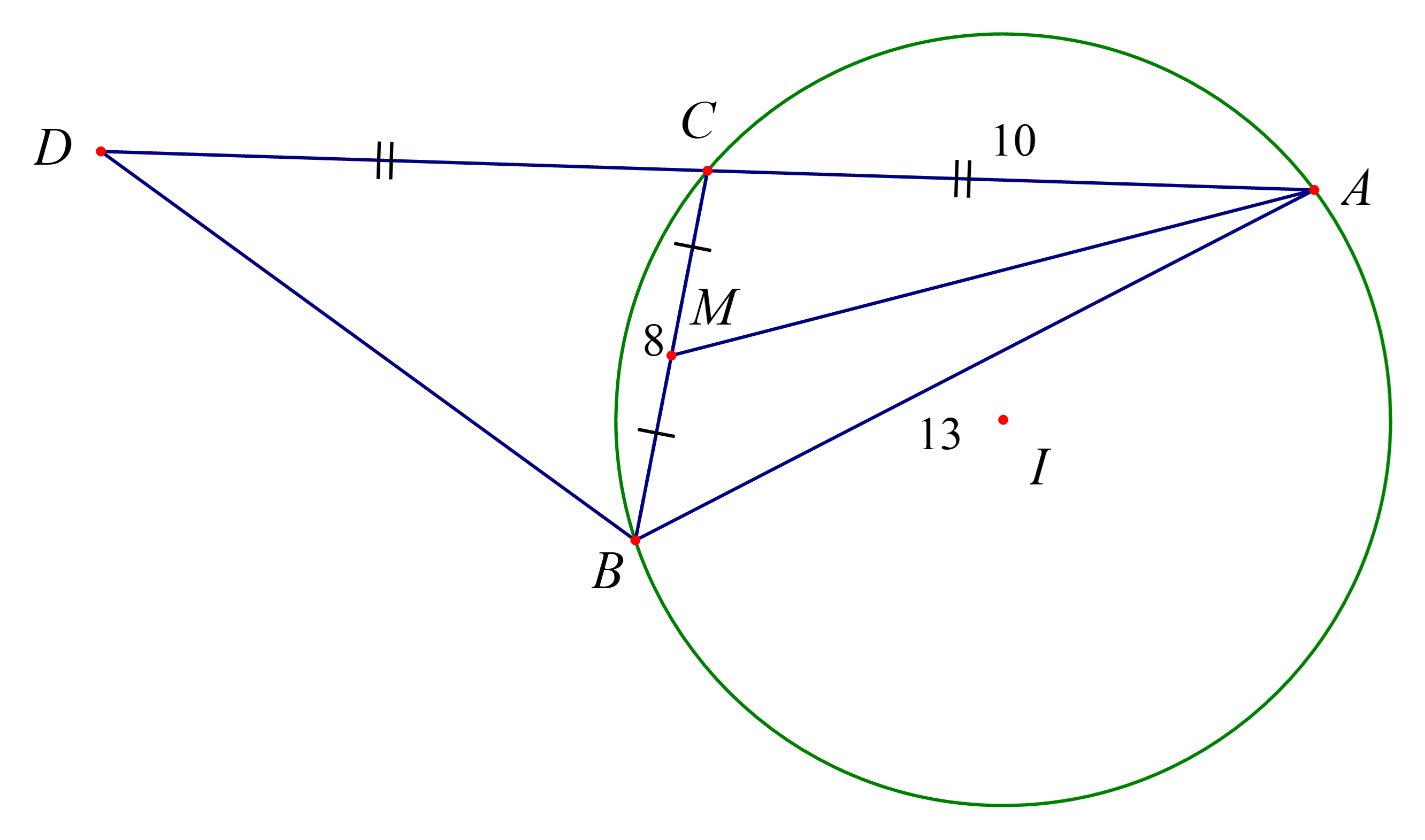
Áp dụng định lí côsin cho tam giác ACM ta có:
AM2 = AC2 + CM2 – 2.AC.CM.cosC = 102 + 42 – 2.10.4.cos91°47'26" = 118,5
⇒ AM ≈ 10,9.
Nửa chu vi của tam giác ABC là :
Áp dụng công thức Heron ta có diện tích tam giác ABC là:
Gọi R là bán kính đường tròn ngoại tiếp tam giác ABC. Khi đó ta có:
Vậy độ dài đường trung tuyến AM ≈ 10,9; diện tích tam giác ABC là 40; bán kính đường tròn ngoại tiếp tam giác ABC là 6,5.
c) Vì D đối xứng với A qua C nên C là trung điểm của AD.
Suy ra AD = 2AC = 2.10 = 20.
Áp dụng hệ quả của định lí côsin cho tam giác ABC ta có:
cosA =
Áp dụng định lí côsin cho tam giác ABD ta có:
BD2 = AD2 + AB2 – 2.AD.AB.cosA = 202 + 132 – 2.20.13. = 159
⇒ BD = ≈ 12,6.
Vậy BD ≈ 12,6.
Lời giải
a) Áp dụng định lí côsin ta có:
a2 = b2 + c2 – 2bccosA = 82 + 52 – 2.8.5.cos120° = 129
⇒ a =
Áp dụng hệ quả của định lí côsin ta có:
cosB =
⇒
Tam giác ABC có:
Vậy a ≈ 11,4; ; .
b) Nửa chu vi tam giác ABC là :
Áp dụng công thức Heron ta có diện tích tam giác ABC:
Vậy diện tích tam giác ABC khoảng 17,2 (đơn vị diện tích).
c) Ta có diện tích tam giác ABC:
Vậy bán kính đường tròn ngoại tiếp tam giác ABC khoảng 6,6 (đơn vị độ dài).
Gọi ha là độ dài đường cao của tam giác ABC hạ từ đỉnh A, tức là ha = AH.
Khi đó
⇒ AH = ha ≈ 3.
Vậy AH ≈ 3.
Lời giải
a) Do ABCD là hình bình hành nên BC = AD; AB = DC,
Và AB // CD nên suy ra cosD = cos(180 – A)= – cosA.
Áp dụng định lí côsin cho hai tam giác ABD và ADC ta có:
BD2 = AD2 + AB2 – 2.AD.AB.cosA = BC2 + AB2 – 2.BC.AB.cosA
AC2 = AD2 + DC2 – 2.AD.DC.cosD = BC2 + AB2 + 2.BC.AB.cosA
Khi đó : BD2 + AC2 = 2AB2 + 2BC2 = 2(AB2 + BC2).
Vậy 2(AB2 + BC2) = AC2 + BD2.
b) Thay AB = 4, BC = 5, BD = 7 vào biểu thức 2(AB2 + BC2) = AC2 + BD2 ta được:
2.(42 + 52) = AC2 + 72 ⇒ AC2 = 2.(42 + 52) – 72 = 33
⇒ AC =
Vậy AC ≈ 5,7.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.