Giải SBT Toán 10 Bài 4. Tích vô hướng của hai vectơ có đáp án
22 người thi tuần này 4.6 577 lượt thi 7 câu hỏi
🔥 Đề thi HOT:
13 câu Trắc nghiệm Tích của vectơ với một số có đáp án (Thông hiểu)
16.8 K lượt thi
13 câu hỏi
16 câu Trắc nghiệm Toán 10 Kết nối tri thức Mệnh đề có đáp án
10.6 K lượt thi
16 câu hỏi
100 câu trắc nghiệm Mệnh đề - Tập hợp nâng cao (P1)
30.2 K lượt thi
20 câu hỏi
28 câu Trắc nghiệm Mệnh đề có đáp án
53.9 K lượt thi
28 câu hỏi
75 câu trắc nghiệm Vectơ nâng cao (P1)
44.3 K lượt thi
25 câu hỏi
100 câu trắc nghiệm Cung và góc lượng giác nâng cao (P1)
18.5 K lượt thi
25 câu hỏi
60 câu Trắc nghiệm Toán 10 Bài hệ thức lượng trong tam giác có đáp án (Mới nhất)
4.3 K lượt thi
60 câu hỏi
100 câu trắc nghiệm Cung và góc lượng giác cơ bản (P1)
30.1 K lượt thi
25 câu hỏi
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
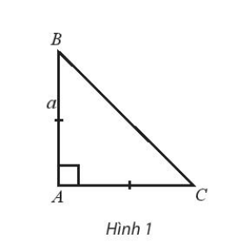
Do tam giác ABC vuông tại A nên AB ⊥ AC ⇒ = 0;
Ta có: CB = = = a
Tam giác ABC vuông cân tại A nên = 45°
Như vậy: = = = = – a. a = –a2
Vậy = 0 và = –a2.
Lời giải
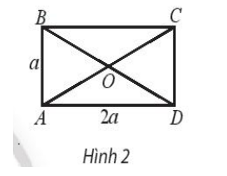
a) Vì ABCD là hình chữ nhật nên AB = CD = a, AD = BC = 2a.
Ta có: AC = = = a.
Xét tam giác BAC vuông tại B, có: cos = cos= .
ABCD là hình chữ nhật nên O là trung điểm của AC và BD
⇒ AO = AC = .
= . . cos = a.. = .
Vậy = .
Lời giải
b) Do ABCD là hình chữ nhật nên ⊥ ⇒ = 0.
Lời giải
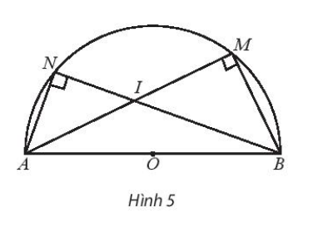
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo