Gọi vị trí của người đo đạc đứng là điểm A và gọi B, C lần lượt là vị trí hai cái cây bên kia sông. Ta có tam giác ABC với AC = 100 m ; AB = 75 m và $\hat{A} = 32^{o}$ .

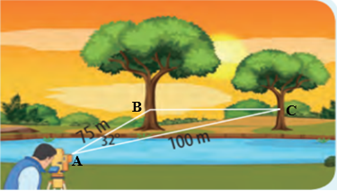
Media VietJack

Áp dụng định lí côsin cho tam giác ABC ta có :

BC² = AB² + AC² – 2.AB.AC.cosA = 75² + 100² – 2.75.100.cos32° ≈ 2 904,3.

⇒ BC ≈ $\sqrt{2904, 3}$ ≈ 53,9 m.

Vậy hai cái cây bên kia sông cách nhau khoảng 53,9 m.

Câu 2

Giải tam giác ABC trong các trường hợp sau:

a) a = 17,4; $\hat{B} = 44^{o} 30'; \hat{C} = 64^{o}$ .

b) a = 10; b = 6; c = 8.

Xem đáp án

Lời giải

a) Tam giác ABC có:

$\hat{A} + \hat{B} + \hat{C} = 180^{o} \Rightarrow \hat{A} = 180^{o} - (\hat{B} + \hat{C}) = 180^{o} - (44^{o} 30' + 64^{o}) = 71^{o} 30'$

Áp dụng định lí sin ta có:

$\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} \Rightarrow \frac{17, 4}{\sin 71^{o} 30'} = \frac{b}{\sin 44^{o} 30'} = \frac{c}{\sin 64^{o}}$

Suy ra:

$b = \frac{17, 4. \sin 44^{o} 30'}{\sin 71^{o} 30'} \approx 12, 9$ ; $c = \frac{17, 4. \sin 64^{o}}{\sin 71^{o} 30'} \approx 16, 5$

Vậy tam giác ABC có: $\hat{A} = 71^{o} 30'$ ; $\hat{B} = 44^{o} 30'; \hat{C} = 64^{o}$ ; a = 17,4; b ≈ 12,9; c ≈ 16,5.

b) Áp dụng hệ quả của định lí côsin ta có:

cosA = $\frac{b^{2} + c^{2} - a^{2}}{2 b c} = \frac{6^{2} + 8^{2} - 10^{2}}{2.6.8} = \frac{0}{96} = 0$

⇒ $\hat{A} = 90^{o}$ .

cosB = $\frac{a^{2} + c^{2} - b^{2}}{2 a c} = \frac{10^{2} + 8^{2} - 6^{2}}{2.10.8} = \frac{128}{160} = 0, 8$

⇒ $\hat{B} \approx 36^{o} 52'$ .

$\hat{A} + \hat{B} + \hat{C} = 180^{o} \Rightarrow \hat{C} = 180^{o} - (\hat{A} + \hat{B}) = 180^{o} - (90^{o} + 36^{o} 52') = 53^{o} 8'$

Vậy tam giác ABC có: $\hat{A} = 90^{o}$ ; $\hat{B} = 36^{o} 52'$ ; $\hat{C} = 53^{o} 8'$ ; a = 10; b = 6; c = 8.

Câu 3

Hai máy bay cùng cất cánh từ một sân bay nhưng bay theo hai hướng khác nhau. Một chiếc di chuyển với vận tốc 450 km/h theo hướng tây và chiếc còn lại di chuyển theo hướng lệch so với hướng bắc 25° về phía tây với tốc độ 630 km/h (Hình 5). Sau 90 phút, hai máy bay cách nhau bao nhiêu kilômét? Giả sử chúng đang ở cùng độ cao.

Xem đáp án

Lời giải

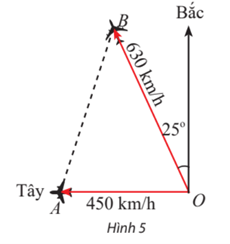
Gọi A và B lần lượt là vị trí của hai máy bay sau khi cất cánh 90 phút.

Đổi 90 phút = 1,5 giờ.

Sau 90 phút (tức là sau 1,5 giờ) chiếc máy bay di chuyển theo hướng tây đi được quãng đường là: 450.1,5 = 675 km, tức là OA = 675 km.

Sau 90 phút (tức là sau 1,5 giờ) chiếc máy bay di chuyển theo hướng lệch bắc 25° về phía tây đi được quãng đường là: 630.1,5 = 945 km, tức là OB = 945 km.

Ta có $\hat{A O B} = 90^{o} - 25^{o} = 65^{o}$ .

Áp dụng định lí côsin cho tam giác OAB ta có:

AB² = OA² + OB² – 2.OA.OB.cos = 675² + 945² – 2.675.945.cos65^o ≈ 809 494,8

⇒ AB = $\sqrt{809 494, 8} \approx 899, 7$ .

Vậy sau 90 phút hai máy bay cách nhau khoảng 899,7 km.

Câu 4

Trên bản đồ địa lí, người ta thường gọi tứ giác với bốn đỉnh lần lượt là các thành phố Hà Tiên, Châu Đốc, Long Xuyên, Rạch Giá là tứ giác Long Xuyên. Dựa theo các khoảng cách đã cho trên Hình 6, tính khoảng cách giữa Châu Đốc và Rạch Giá.

Xem đáp án

Lời giải

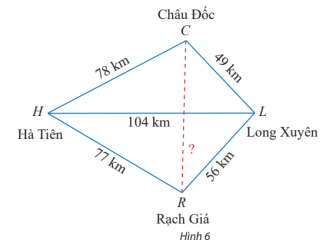
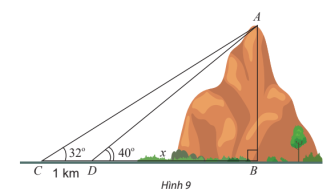
Áp dụng hệ quả của định lí côsin cho tam giác CHL ta có:

cos $\hat{C L H}$ =

$\frac{C L^{2} + H L^{2} - C H^{2}}{2. C L . H L} = \frac{49^{2} + 104^{2} - 78^{2}}{2.49.104} \approx 0, 6999$

⇒ $\hat{C L H}$ ≈ 45°35'.

Áp dụng hệ quả của định lí côsin cho tam giác RHL ta có:

cos $\hat{R L H}$ =

$\frac{R L^{2} + H L^{2} - R H^{2}}{2. R L . H L} = \frac{56^{2} + 104^{2} - 77^{2}}{2.56.104} \approx 0, 6888$

⇒ $\hat{R L H}$ ≈ 46°28'.

Suy ra $\hat{C L R} = \hat{C L H} + \hat{R L H} \approx 45^{o} 35 ’ + 46^{o} 28 ’ \approx 92^{o} 3'$

Áp dụng định lí côsin cho tam giác LCR ta có:

CR² = CL² + LR² – 2.CL.LR.cos $\hat{C L R}$ = 49² + 56² – 2.49.56.cos92^o3’ ≈ 5 733,3

⇒ CR ≈ 75,7.

Vậy khoảng cách giữa Châu Đốc và Rạch Giá khoảng 75,7 km.

Câu 5

Giải tam giác ABC trong các trường hợp sau:

a) AB = 14, AC = 23, $\hat{A} = 125^{o}$ ;

b) BC = 22, $\hat{B} = 64^{o}, \hat{C} = 38^{o}$ ;

c) AC = 22, $\hat{B} = 120^{o}, \hat{C} = 28^{o}$ ;

d) AB = 23, AC = 32, BC = 44.

Xem đáp án

Lời giải

a) Áp dụng định lí côsin cho tam giác ABC ta có:

BC² = AB² + AC² – 2.AB.AC.cosA = 14² + 23² – 2.14.23.cos125° ≈ 1 094,4.

⇒ BC ≈ $\sqrt{1 094, 4} \approx 33, 1$ .

Áp dụng hệ quả của định lí côsin cho tam giác ABC ta có:

cosB = $\frac{A B^{2} + B C^{2} - A C^{2}}{2. A B . B C} = \frac{14^{2} + 33, 1^{2} - 23^{2}}{2.14.33, 1} \approx 0, 823$

⇒ $\hat{B} \approx 34^{o} 37'$

Mặt khác tam giác ABC có:

$\hat{A} + \hat{B} + \hat{C} = 180^{o} \Rightarrow \hat{C} = 180^{o} - (\hat{A} + \hat{B}) = 180^{o} - (125^{o} + 34^{o} 37') = 20^{o} 23'$

Vậy tam giác ABC có:

AB = 14, AC = 23, BC ≈ 33,1; $\hat{A} = 125^{o}$ ; $\hat{B} \approx 34^{o} 37'$ ; $\hat{C} \approx 20^{o} 23'$ .

b) Tam giác ABC có:

$\hat{A} + \hat{B} + \hat{C} = 180^{o} \Rightarrow \hat{A} = 180^{o} - (\hat{B} + \hat{C}) = 180^{o} - (64^{o} + 38^{o}) = 78^{o}$

Áp dụng định lí sin cho tam giác ABC ta có:

$\frac{B C}{\sin A} = \frac{A C}{\sin B} = \frac{A B}{\sin C} \Rightarrow \frac{22}{\sin 78^{o}} = \frac{A C}{\sin 64^{o}} = \frac{A B}{\sin 38^{o}}$

Suy ra: $A C = \frac{22. \sin 64^{o}}{\sin 78^{o}} \approx 20, 2$ ; $A B = \frac{22. \sin 38^{o}}{\sin 78^{o}} \approx 13, 8$

Vậy tam giác ABC có:

$\hat{A} = 78^{o}; \hat{B} = 64^{o}, \hat{C} = 38^{o}$ ; AB ≈ 13,8; AC ≈ 20,2; BC = 22.

c) Tam giác ABC có:

$\hat{A} + \hat{B} + \hat{C} = 180^{o} \Rightarrow \hat{A} = 180^{o} - (\hat{B} + \hat{C}) = 180^{o} - (120^{o} + 28^{o}) = 32^{o}$

Áp dụng định lí sin cho tam giác ABC ta có:

$\frac{B C}{\sin A} = \frac{A C}{\sin B} = \frac{A B}{\sin C} \Rightarrow \frac{B C}{\sin 32^{o}} = \frac{22}{\sin 120^{o}} = \frac{A B}{\sin 28^{o}}$

Suy ra: $B C = \frac{22. \sin 32^{o}}{\sin 120^{o}} \approx 13, 5$ ; $A B = \frac{22. \sin 28^{o}}{\sin 120^{o}} \approx 11, 9$

Vậy tam giác ABC có:

$\hat{A} = 32^{o}; \hat{B} = 120^{o}, \hat{C} = 28^{o}$ ; AB ≈ 11,9; AC = 22; BC = 13,5.

d) Áp dụng hệ quả của định lí côsin ta có:

cosA = $\frac{A B^{2} + A C^{2} - B C^{2}}{2. A B . A C} = \frac{23^{2} + 32^{2} - 44^{2}}{2.23.32} = \frac{- 383}{1472} \approx - 0, 26$

⇒ $\hat{A} \approx 105^{o} 4'$

cosB =

$\frac{A B^{2} + B C^{2} - A C^{2}}{2. A B . B C} = \frac{23^{2} + 44^{2} - 32^{2}}{2.23.44} = \frac{1441}{2024} \approx 0, 712$

⇒ $\hat{B} = 44^{o} 36'$

$\hat{A} + \hat{B} + \hat{C} = 180^{o} \Rightarrow \hat{C} = 180^{o} - (\hat{A} + \hat{B}) = 180^{o} - (105^{o} 4' + 44^{o} 36') = 30^{o} 20'$

Vậy tam giác ABC có: $\hat{A} \approx 105^{o} 4'$ ; $\hat{B} = 44^{o} 36'$ ; $\hat{C} = 30^{o} 20'$ ; AB = 23, AC = 32, BC = 44.

Câu 6

Để lắp đường dây điện cao thế từ vị trí A đến vị trí B, do phải tránh một ngọn núi nên người ta phải nối đường dây từ vị trí A đến vị trí C dài 10 km, sau đó nối đường dây từ vị trí C đến vị trí B dài 8 km. Góc tạo bởi hai đoạn dây AC và CB là 70°. Tính chiều dài tăng thêm vì không thể nối trực tiếp từ A đến B.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Một người đứng cách thân một cái quạt gió 16 m và nhìn thấy tâm của cánh quạt với góc nâng 56,5° (Hình 8). Tính khoảng cách từ tâm của cánh quạt đến mặt đất. Cho biết khoảng cách từ mắt của người đó đến mặt đất là 1,5 m.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 8

Tính chiều cao AB của một ngọn núi. Biết tại hai điểm C, D cách nhau 1 km trên mặt đất (B, C, D thẳng hàng), người ta nhìn thấy đỉnh A của núi với góc nâng lần lượt là 32° và 40° (Hình 9).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 9

Hai người quan sát khinh khí cầu tại hai địa điểm P và Q nằm ở sườn đồi nghiêng 32° so với phương ngang, cách nhau 60 m (Hình 10). Người quan sát tại P xác định góc nâng của khinh khí cầu là 62°. Cùng lúc đó, người quan sát tại Q xác định góc nâng của khinh khí cầu đó là 70°. Tính khoảng cách từ Q đến khinh khí cầu.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 10

Một người đứng ở trên một tháp truyền hình cao 352 m so với mặt đất, muốn xác định khoảng cách giữa hai cột mốc trên mặt đất bên dưới. Người đó quan sát thấy góc được tạo bởi hai đường ngắm tới hai mốc này là 43°, góc giữa phương thẳng đứng và đường ngắm tới một điểm mốc trên mặt đất là 62° và điểm mốc khác là 54° (Hình 11). Tính khoảng cách giữa hai cột mốc này.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Tiếng Anh

Giáo dục Kinh tế và Pháp luật

ĐHQG Hồ Chí Minh

ĐH Bách Khoa

ĐHQG Hà Nội

Bộ Công an

ĐHSP Hà Nội

Bằng lái xe

English Test

IT Test

Đại học

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Tin học

Giáo dục Kinh tế và Pháp luật

Global success

iLearn Smart World

Friends Global

Explore new worlds

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử