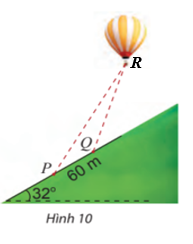
Tính chiều cao AB của một ngọn núi. Biết tại hai điểm C, D cách nhau 1 km trên mặt đất (B, C, D thẳng hàng), người ta nhìn thấy đỉnh A của núi với góc nâng lần lượt là 32° và 40° (Hình 9).
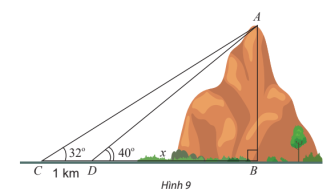
Tính chiều cao AB của một ngọn núi. Biết tại hai điểm C, D cách nhau 1 km trên mặt đất (B, C, D thẳng hàng), người ta nhìn thấy đỉnh A của núi với góc nâng lần lượt là 32° và 40° (Hình 9).
Câu hỏi trong đề: Bài tập Giải tam giác và ứng dụng thực tế có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đặt BD = x km, khi đó ta có CB = BD + CD = x + 1.
Trong tam giác ABC vuông tại B ta có: (1)
Trong tam giác ABD vuông tại B ta có:
(2)
Từ (1) và (2) suy ra:
Suy ra AB = x.tan40° ≈ 2,92.tan40° ≈ 2,45 km.
Vậy chiều cao AB của một ngọn núi khoảng 2,45 km.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
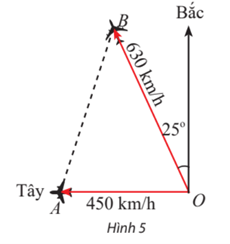
Gọi A và B lần lượt là vị trí của hai máy bay sau khi cất cánh 90 phút.
Đổi 90 phút = 1,5 giờ.
Sau 90 phút (tức là sau 1,5 giờ) chiếc máy bay di chuyển theo hướng tây đi được quãng đường là: 450.1,5 = 675 km, tức là OA = 675 km.
Sau 90 phút (tức là sau 1,5 giờ) chiếc máy bay di chuyển theo hướng lệch bắc 25° về phía tây đi được quãng đường là: 630.1,5 = 945 km, tức là OB = 945 km.
Ta có .
Áp dụng định lí côsin cho tam giác OAB ta có:
AB2 = OA2 + OB2 – 2.OA.OB.cos = 6752 + 9452 – 2.675.945.cos65o ≈ 809 494,8
⇒ AB = .
Vậy sau 90 phút hai máy bay cách nhau khoảng 899,7 km.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
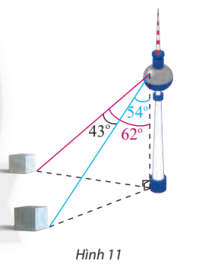
Gọi vị trí người đứng ở trên tháp truyền hình là A, hai cột mốc ở dưới đất lần lượt là B và C, chân tháp truyền hình là D.
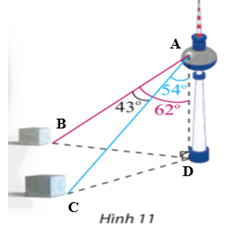
Khi đó ta có các tam giác ABD và ACD vuông tại D.
; AD = 352 m.
Trong tam giác ABD vuông tại D ta có:
Trong tam giác ACD vuông tại D ta có:
Áp dụng định lí côsin cho tam giác ABC ta có:
BC2 = AB2 + AC2 – 2.AB.AC. cos
= 749,82 + 598,92 – 2.749,8.598,9. cos43° ≈ 264 044,9
⇒ BC = m.
Vậy khoảng cách giữa hai cột mốc khoảng 513,9 m.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập