Giải SBT Toán 10 Bài 2. Định lí côsin và định lí sin có đáp án

Lời giải

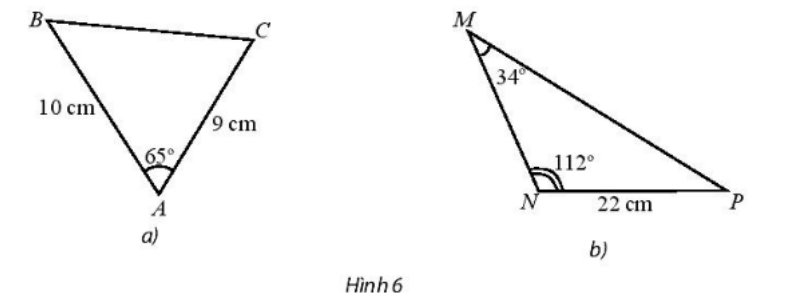
a) Áp dụng định lí côsin ta có:

BC² = AB² + AC² – 2.AB.AC.cos\(\widehat {\rm{A}}\)

BC² = 10² + 9² – 2.10.9.cos65°

BC ² ≈ 104,929

BC ≈ 10,24 (cm).

Vậy BC ≈ 10,24 (cm).

b) \(\widehat {\rm{P}}\)= 180° – 112° – 34° = 34°.

Ta có: \(\widehat {\rm{P}}\) = \(\widehat {\rm{M}}\) ⇒ tam giác MNP cân tại N ⇒ MN = NP = 22 (cm)

Áp dụng định lí sin ta có: \(\frac{{{\rm{MP}}}}{{{\rm{sinN}}}}{\rm{ = }}\frac{{{\rm{MN}}}}{{{\rm{sinP}}}}{\rm{ = }}\frac{{{\rm{NP}}}}{{{\rm{sinM}}}} = \frac{{22}}{{\sin 34^\circ }}\).

⇒ MP = \(\frac{{22}}{{\sin 34^\circ }}\).sin112° ≈ 36,48 (cm)

Vậy MP ≈ 36,48 cm, MN = 22 cm.

R = \(\frac{{\rm{a}}}{{{\rm{2sinA}}}}\) = \(\frac{{75}}{{2.\sin 60^\circ }}\) = 25\(\sqrt 3 \) (cm).

Vậy R = 25\(\sqrt 3 \) cm.

Lời giải

Do b là cạnh lớn nhất nên B là góc lớn nhất.

Theo định lí côsin: b² = a² + c² – 2accosB

⇒ cosB = \[\frac{{{{\rm{a}}^2} + {{\rm{c}}^2} - {{\rm{b}}^2}}}{{2{\rm{ac}}}}\] = \(\frac{{{8^2} + {6^2} - {{12}^2}}}{{2.8.6}}\)

⇒ cosB = \(\frac{{ - 11}}{{24}}\).

⇒ \(\widehat {\rm{B}}\) = 117°16’46’’.

Vậy góc lớn nhất của tam giác ABC là \(\widehat {\rm{B}}\) = 117°16’46’’.

Lời giải

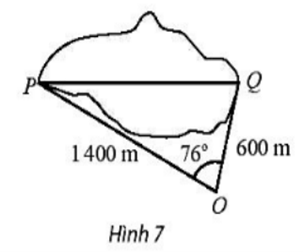
Áp dụng định lí côsin:

PQ² = OP² + OQ² – 2.OP.OQ.cos\(\widehat {\rm{O}}\)

PQ² = 1400² + 600² – 2.1400.600.cos76°

PQ = \(\sqrt {{{1400}^2} + {{600}^2}--{\rm{ }}2.1400.600.{\rm{cos}}76^\circ } \)

PQ ≈ 1383,32 (m).

Vậy khoảng cách giữa hai điểm PQ là PQ ≈ 1383,32 (m).

Lời giải

Theo định lí côsin ta có: a² = b² + c² – 2bccosA

⇒ cosA = \(\frac{{{{\rm{b}}^2} + {{\rm{c}}^2} - {{\rm{a}}^2}}}{{{\rm{2bc}}}}\)

Ta có:

1 + cosA = 1 + \(\frac{{{{\rm{b}}^2} + {{\rm{c}}^2} - {{\rm{a}}^2}}}{{{\rm{2bc}}}}\) = \(\frac{{2{\rm{bc}} + {{\rm{b}}^2} + {{\rm{c}}^2} - {{\rm{a}}^2}}}{{2{\rm{bc}}}}\) = \(\frac{{{{({\rm{b}} + {\rm{c}})}^2} - {{\rm{a}}^2}}}{{2{\rm{bc}}}}\) = \(\frac{{({\rm{a}} + {\rm{b}} + {\rm{c}})( - {\rm{a}} + {\rm{b}} + {\rm{c}})}}{{2{\mathop{\rm bc}\nolimits} }}\)

Vậy ta có điều phải chứng minh.