Câu hỏi:
13/07/2024 1,630Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
Áp dụng định lí côsin:
NP2 = MP2 + MN2 – 2.MN.MP.cos\(\widehat {\rm{M}}\)
NP2 = 102 + 202 – 2.10.20.cos42°
NP = \(\sqrt {{{10}^2} + {\rm{ }}{{20}^2}--{\rm{ }}2.10.20.{\rm{cos}}42^\circ } \)
NP ≈ 14,24.
Áp dụng định lí sin trong tam giác MNP, ta có: R = ON = OP = \(\frac{{{\rm{NP}}}}{{{\rm{2sin}}\widehat {\rm{M}}}}\) ≈ \(\frac{{14,24}}{{2\sin 42^\circ }}\) ≈ 10,64
Xét đường tròn tâm O ngoại tiếp tam giác MNP:
\[\widehat {{\rm{NMP}}}\] là góc nội tiếp chắn cung NP ⇒ \[\widehat {{\rm{NMP}}}\] = \(\frac{1}{2}\)\(\widehat {{\rm{NOP}}}\) ⇒ \(\widehat {{\rm{NOP}}}\) = 42°.2 = 84°.
Suy ra SONP = \(\frac{1}{2}\).ON.OP.sin\(\widehat {{\rm{NOP}}}\) ≈ \(\frac{1}{2}\).(10,64)2.sin84° ≈ 56,30 (đvdt)
Vậy diện tích tam giác ONP là 56,30 đvdt.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
Theo định lí côsin ta có: a2 = b2 + c2 – 2bccosA
⇒ cosA = \(\frac{{{{\rm{b}}^2} + {{\rm{c}}^2} - {{\rm{a}}^2}}}{{{\rm{2bc}}}}\)
Ta có:
1 + cosA = 1 + \(\frac{{{{\rm{b}}^2} + {{\rm{c}}^2} - {{\rm{a}}^2}}}{{{\rm{2bc}}}}\) = \(\frac{{2{\rm{bc}} + {{\rm{b}}^2} + {{\rm{c}}^2} - {{\rm{a}}^2}}}{{2{\rm{bc}}}}\) = \(\frac{{{{({\rm{b}} + {\rm{c}})}^2} - {{\rm{a}}^2}}}{{2{\rm{bc}}}}\) = \(\frac{{({\rm{a}} + {\rm{b}} + {\rm{c}})( - {\rm{a}} + {\rm{b}} + {\rm{c}})}}{{2{\mathop{\rm bc}\nolimits} }}\)
Vậy ta có điều phải chứng minh.
Lời giải
Lời giải
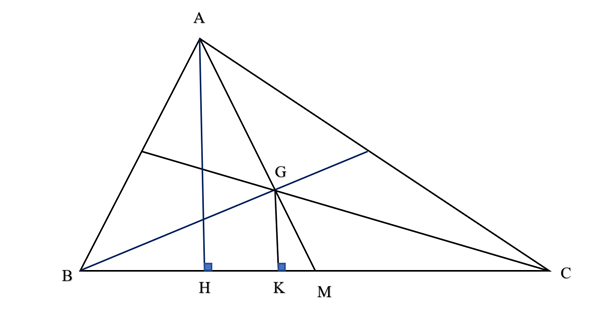
Vẽ AH và GK vuông góc với BC.
Gọi M là chân đường trung tuyến từ A hạ xuống BC. Ta có GM = \(\frac{1}{3}\)AM ( tính chất đường trung tuyến của tam giác).
Xét tam giác GKM và tam giác AHM:
\(\widehat {{\rm{AHM}}}\) = \(\widehat {{\rm{GKM}}}\) = 90°
\(\widehat {{\rm{AMH}}}\) = \(\widehat {{\rm{GMK}}}\)
⇒ tam giác GKM và tam giác AHM đồng dạng (g.g).
⇒ \(\frac{{{\rm{GM}}}}{{{\rm{AM}}}} = \frac{{{\rm{GK}}}}{{{\rm{AH}}}} = \frac{1}{3}\)
Có \(\frac{{{{\rm{S}}_{{\rm{GBC}}}}}}{{{{\rm{S}}_{{\rm{ABC}}}}}}{\rm{ = }}\frac{{\frac{{\rm{1}}}{{\rm{2}}}{\rm{.GK}}{\rm{.BC}}}}{{\frac{{\rm{1}}}{{\rm{2}}}{\rm{.AH}}{\rm{.BC}}}}\) = \(\frac{{{\rm{GK}}}}{{{\rm{AH}}}} = \frac{1}{3}\).
Chứng minh tương tự ta được:
SGBC = SGAB = SGAC = \(\frac{1}{3}\)SABC. ( ĐPCM).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
13 câu Trắc nghiệm Tích của vectơ với một số có đáp án (Thông hiểu)
-
12 Bài tập Ứng dụng của hàm số bậc hai để giải bài toán thực tế (có lời giải)
-
16 câu Trắc nghiệm Toán 10 Kết nối tri thức Mệnh đề có đáp án
-
10 Bài tập Ứng dụng ba đường conic vào các bài toán thực tế (có lời giải)
-
Bộ 2 Đề kiểm tra giữa học kì 2 Toán 10 Kết nối tri thức có đáp án - Đề 1
-
10 Bài tập Tìm hệ số, số hạng trong khai triển nhị thức Newton (có lời giải)
-
10 Bài tập Cách xét tính đúng sai của mệnh đề (có lời giải)
-
15 câu Trắc nghiệm Toán 10 chân trời sáng tạo Không gian mẫu và biến cố có đáp án