Bài tập Các số đặc trưng đo mức độ phân tán của mẫu số liệu có đáp án

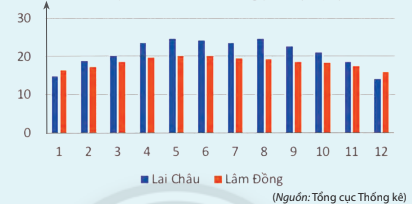
Địa phương có thời tiết ôn hòa hơn là nơi nhiệt độ thay đổi ít hơn hay chênh lệch nhiệt độ giữa các tháng ít hơn.

Quan sát biểu đồ ta thấy các cột màu cam (thể hiện nhiệt độ không khí trung bình các tháng trong năm 2019 tại Lâm Đồng) hầu như ngang bằng nhau hơn so với các cột màu xanh (thể hiện nhiệt độ không khí trung bình các tháng trong năm 2019 tại Lai Châu) nên ta có thể dự đoán thời tiết ở Lâm Đồng ôn hòa hơn.

a) Ở nhóm 1, người chạy nhanh nhất để hoàn thành 5 km là người có thời gian chạy ít nhất và thời gian chạy đó là 17 phút, người chạy chậm nhất là người có thời gian chạy nhiều nhất và thời gian chạy đó là 47 phút.

Vậy độ chênh lệch giữa thời gian chạy của người nhanh nhất và người chậm nhất trong nhóm 1 là: 47 – 17 = 30 phút.

Ở nhóm 2, người chạy nhanh nhất để hoàn thành 5 km là người có thời gian chạy ít nhất và thời gian chạy đó là 29 phút, người chạy chậm nhất là người có thời gian chạy nhiều nhất và thời gian chạy đó là 32 phút.

Vậy độ chênh lệch giữa thời gian chạy của người nhanh nhất và người chậm nhất trong nhóm 2 là: 32 – 29 = 3 phút.

b) Quan sát qua thời gian chạy của các thành viên trong hai nhóm thì ta thấy nhóm 2 có thành tích chạy đồng đều hơn vì thời gian chạy của các thành viên ở xung quang từ 29 đến 32 và độ chênh lệch thời gian giữa người chạy nhanh nhất và chậm nhất thấp.

a) Sắp xếp mẫu số liệu theo thứ tự không giảm, ta được:

2; 2; 5; 7; 10; 10; 13; 15; 19.

+ Khoảng biến thiên của mẫu số liệu là: R = 19 – 2 = 17.

+ Cỡ mẫu là n = 9 là số lẻ nên giá trị tứ phân vị thứ hai là: Q₂ = 10.

+ Tứ phân vị thứ nhất là trung vị của mẫu: 2; 2; 5; 7. Do đó Q₁ = 3,5.

+ Tứ phân vị thứ ba là trung vị của mẫu: 10; 13; 15; 19. Do đó Q₃ = 14.

+ Khoảng tứ phân vị của mẫu là: ∆_Q = 14 – 3,5 = 10,5.

b) Sắp xếp mẫu số liệu theo thứ tự không giảm, ta được:

1; 2; 5; 5; 9; 10; 10; 15; 15; 19.

+ Khoảng biến thiên của mẫu số liệu là: R = 19 – 1 = 18.

+ Cỡ mẫu là n = 10 là số chẵn nên giá trị tứ phân vị thứ hai là: Q₂ = $\frac{1}{2}(9+10)=9,5$.

+ Tứ phân vị thứ nhất là trung vị của mẫu: 1; 2; 5; 5; 9. Do đó Q₁ = 5.

+ Tứ phân vị thứ ba là trung vị của mẫu: 10; 10; 15; 15; 19. Do đó Q₃ = 15.

+ Khoảng tứ phân vị của mẫu là: ∆_Q = 15 – 5 = 10.

a)

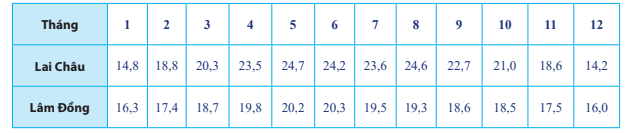
* Tỉnh Lai Châu:

Sắp xếp các số liệu theo thứ tự không giảm, ta được:

14,2; 14,8; 18,6; 18,8; 20,3; 21,0; 22,7; 23,5; 23,6; 24,2; 24,6; 24,7.

+ Khoảng biến thiên của mẫu số liệu là: R = 24,7 – 14,2 = 10,5.

+ Cỡ mẫu là n = 12 là số chẵn nên giá trị tứ phân vị thứ hai là:

Q₂ = $\frac{1}{2}(21,0+22,7)=21,85$.

+ Tứ phân vị thứ nhất là trung vị của mẫu: 14,2; 14,8; 18,6; 18,8; 20,3; 21,0.

Do đó Q₁ = $\frac{1}{2}(18,6+18,8)=18,7$.

+ Tứ phân vị thứ ba là trung vị của mẫu: 22,7; 23,5; 23,6; 24,2; 24,6; 24,7.

Do đó Q₃ = $\frac{1}{2}(23,6+24,2)=23,9$.

+ Khoảng tứ phân vị của mẫu là: ∆_Q = 23,9 – 18,7 = 5,2.

* Tỉnh Lâm Đồng:

Sắp xếp các số liệu theo thứ tự không giảm, ta được:

16,0; 16,3; 17,4; 17,5; 18,5; 18,6; 18,7; 19,3; 19,5; 19,8; 20,2; 20,3.

+ Khoảng biến thiên của mẫu số liệu là: R' = 20,3 – 16,0 = 4,3.

+ Cỡ mẫu là n = 12 là số chẵn nên giá trị tứ phân vị thứ hai là:

Q'₂ = $\frac{1}{2}(18,6+18,7)=18,65$.

+ Tứ phân vị thứ nhất là trung vị của mẫu: 16,0; 16,3; 17,4; 17,5; 18,5; 18,6.

Do đó Q'₁ = $\frac{1}{2}(17,4+17,5)=17,45$.

+ Tứ phân vị thứ ba là trung vị của mẫu: 18,7; 19,3; 19,5; 19,8; 20,2; 20,3.

Do đó Q'₃ = $\frac{1}{2}(19,5+19,8)=19,65$.

+ Khoảng tứ phân vị của mẫu là: ∆'_Q = 19,65 – 17,45 = 2,2.

b) Xét về cả khoảng biến thiên và khoảng tứ phân vị của nhiệt độ trung bình mỗi tháng của cả hai tỉnh, ta thấy: 10,5 > 4,3 hay R > R' và 5,2 > 2,2 hay ∆_Q > ∆'_Q.

Điều đó có nghĩa là trong một năm, nhiệt độ ở Lâm Đồng ít thay đổi hơn.

Sắp xếp các số liệu theo thứ tự không giảm, ta được:

3; 3; 9; 9; 10; 10; 12; 12; 37.

+ Vì cỡ mẫu là n = 9 lá số lẻ nên giá trị tứ phân vị thứ hai là Q₂ = 10.

+ Tứ phân vị thứ nhất là trung vị của mẫu: 3; 3; 9; 9. Do đó Q₁ = 6.

+ Tứ phân vị thứ ba là trung vị của mẫu: 10; 12; 12; 37. Do đó Q₃ = 12.

+ Khoảng tứ phân vị của mẫu là: ∆_Q = 12 – 6 = 6.

Ta có: Q₃ + 1,5∆_Q = 12 + 1,5 . 6 = 21 và Q₁ – 1,5∆_Q = 6 – 1,5 . 6 = – 3.

Do đó mẫu có một giá trị ngoại lệ là 37.