Giải SBT Toán 10 Bài 2. Hàm số bậc hai có đáp án

Hướng dẫn giải

+ Hàm số a) có dạng y = ax² + bx + c với a = 3 ≠ 0, b = 1 và c = \( - \sqrt 3 \) nên đây là hàm số bậc hai.

+ Hàm số b) không phải là hàm số bậc hai vì công thức của hàm số có chứa dấu giá trị tuyệt đối.

+ Hàm số c) không phải là hàm số bậc hai vì hàm số này được cho bởi hai công thức.

+ Ta có y = 2(x² + 1) + 3x – 1 hay y = 2x² + 3x + 1 nên hàm số d) là hàm số bậc hai vì nó có dạng y = ax² + bx + c với a = 2 ≠ 0, b = 3 và c = 1.

Vậy trong các hàm số đã cho, hàm số b) và hàm số c) không phải là hàm số bậc hai.

Hướng dẫn giải

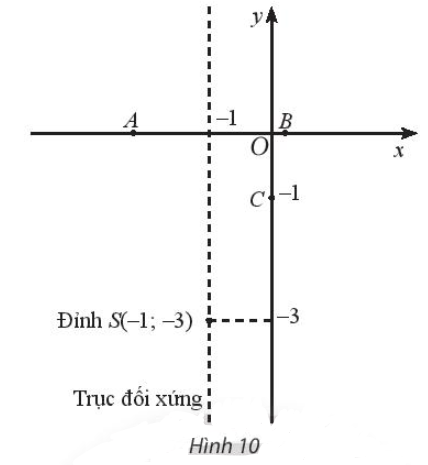
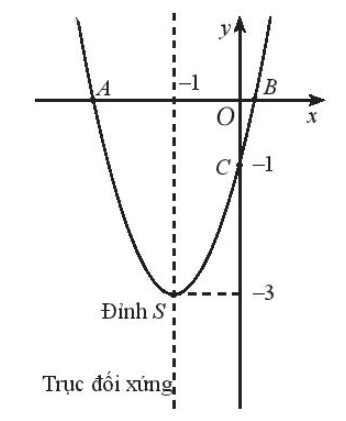
Ta vẽ parabol có bề lõm hướng lên trên và đi qua các điểm A, S, C, B, ta được đồ thị của hàm số đã cho như sau:

Hướng dẫn giải

Hướng dẫn giải

Hàm số bậc hai có công thức tổng quát: y = ax² + bx + c (a ≠ 0).

Đồ thị hàm số đi qua điểm A(1; – 3) nên: – 3 = a . 1² + b . 1 + c hay a + b + c = – 3. (1)

Đồ thị hàm số đi qua điểm B(0; – 2) nên: – 2 = a . 0² + b . 0 + c hay c = – 2.

Đồ thị hàm số đi qua điểm C(2; – 10) nên: – 10 = a . 2² + b . 2 + c hay 4a + 2b + c = – 10. (2).

Thay c = – 2 vào (1) ta được: a + b – 2 = – 3 ⇔ a + b = – 1 ⇔ a = – 1 – b. (3)

Thay c = – 2 vào (2) ta được: 4a + 2b – 2 = – 10 ⇔ 4a + 2b = – 8 ⇔ 2a + b = – 4. (4)

 Thay (3) vào (4) ta được: 2.(– 1 – b) + b = – 4 ⇔ – 2 – 2b + b = – 4 ⇔ b = 2.

Thay b = 2 vào (3) ta được: a = – 1 – 2 = – 3 (t/m).

Vậy công thức hàm số là y = – 3x² + 2x – 2.