Bài tập Phương pháp quy nạp toán học có đáp án

Hướng dẫn giải

Có thể kết luận rằng tất cả các quân domino đều đổ. Vì: quân domino đầu tiên đổ thì sử dụng 2) ta có quân domino thứ 2 cũng đổ, quân domino thứ 2 đổ thì lại tiếp tục sử dụng 2) suy ra quân domino thứ 3 cũng đổ,...cứ như vậy quân domino cuối cùng cũng đổ. Do đó tất cả các quân domino đều đổ.

Hướng dẫn giải

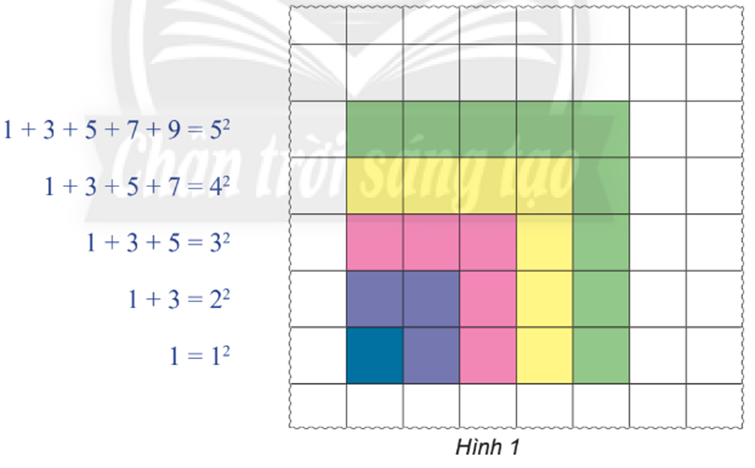
a) Với n = 1, ta có 2.1 – 1 = 1 = 12, do đó công thức (1) đúng với n = 1.

Với n = 2, ta có 1 + (2.2 – 1) = 4 = 22, do đó công thức (1) đúng với n = 2.

Với n = 3, ta có 1 + 3 + (2.3 – 1) = 9 = 32, do đó công thức (1) đúng với n = 3.

Với n = 4, ta có 1 + 3 + 5 + (2.4 – 1) = 16 = 42, do đó công thức (1) đúng với n = 4.

Với n = 5, ta có 1 + 3 + 5 + 7 + (2.5 – 1) = 25 = 52, do đó công thức (1) đúng với n = 5.

b) Mỗi lần tô thêm một hàng và cột những ô vuông, bạn học sinh đã kiểm nghiệm công thức (1) thêm một trường hợp của n. Tuy nhiên, bới tập hợp ℕ* là vô hạn nên cách làm đó không thể chứng tỏ công thức (1) đúng với mọi n $\in$ ℕ*.

Hướng dẫn giải

Bước 1. Với n = 1, ta có 1 = $\frac{1(1+1)}{2}.$ Do đó đẳng thức đúng với n = 1.

Bước 2. Giả sử đẳng thức đúng với n = k ≥ 1, nghĩa là có: $1+2+3+\dots +k=\frac{k(k+1)}{2}.$

Ta cần chứng minh đẳng thức đúng với n = k + 1, nghĩa là cần chứng minh:$1+2+3+\dots +k+(k+1)=\frac{(k+1)\left[(k+1)+1\right]}{2}.$

Sử dụng giả thiết quy nạp, ta có:

$1+2+3+\mathrm{...}+k+(k+1)$

$=\frac{k(k+1)}{2}+\frac{2(k+1)}{2}=\frac{(k+1)(k+2)}{2}=\frac{(k+1)[(k+1)+1]}{2}.$

Vậy đẳng thức đúng với n = k + 1.

Theo nguyên lí quy nạp toán học, đẳng thức đúng với mọi số tự nhiên n ≥ 1.

Hướng dẫn giải

Bước 1. Với n = 3, ta có 23 + 1 = 16 > 14 = 32 + 3 + 2. Do đó bất đẳng thức đúng với n = 3.

Bước 2. Giả sử bất đẳng thức đúng với n = k ≥ 3, nghĩa là có: 2k + 1 > k2 + k + 2.

Ta cần chứng minh đẳng thức đúng với n = k + 1, nghĩa là cần chứng minh:

2(k +1) + 1 > (k + 1)² + (k + 1) + 2.

Sử dụng giả thiết quy nạp, với lưu ý k ≥ 3, ta có:

2(k +1) + 1 = 2 . 2k + 1 > 2(k2 + k + 2) = 2k² + 2k + 4 = k² + k² + 2k + 4 > k² + k + 2k + 4

= (k² + 2k + 1) + (k + 1) + 2 = (k + 1)² + (k + 1) + 2.

Vậy bất đẳng thức đúng với n = k + 1.

Theo nguyên lí quy nạp toán học, bất đẳng thức đúng với mọi số tự nhiên n ≥ 3.

Hướng dẫn giải

Bước 1. Với n = 1, ta có 13 + 2 . 1 = 3 ⁝ 3. Do đó khẳng định đúng với n = 1.

Bước 2. Giả sử khẳng định đúng với n = k ≥ 1, nghĩa là có: k3 + 2k ⁝ 3.

Ta cần chứng minh đẳng thức đúng với n = k + 1, nghĩa là cần chứng minh:

(k + 1)³ + 2(k + 1) ⁝ 3.

Sử dụng giả thiết quy nạp, ta có:

(k + 1)³ + 2(k + 1) = k³ + 3k² + 3k + 1 + 2k + 2 = (k³ + 2k) + (3k² + 3k + 3)

Vì (k³ + 2k) và (3k² + 3k + 3) đều chia hết cho 3 nên (k³ + 2k) + (3k² + 3k + 3) ⁝ 3 hay (k + 1)3 + 2(k + 1) ⁝ 3.

Vậy khẳng định đúng với n = k + 1.

Theo nguyên lí quy nạp toán học, khẳng định đúng với mọi số tự nhiên n ≥ 1.

Hướng dẫn giải

Bước 1. Với n = 1, ta có q1 – 1 = q0 = 1 = $\frac{1-q}{1-q}=\frac{1-q^1}{1-q}.$ Do đó đẳng thức đúng với n = 1.

Bước 2. Giả sử đẳng thức đúng với n = k ≥ 1, nghĩa là có:

$1+q+q^2+q^3+q^4+\dots +q^{k-1}=\frac{1-q^k}{1-q}.$

Ta cần chứng minh đẳng thức đúng với n = k + 1, nghĩa là cần chứng minh:$1+q+q^2+q^3+q^4+\dots +q^{k-1}+q^{(k+1)-1}=\frac{1-q^{k+1}}{1-q}.$

Sử dụng giả thiết quy nạp, ta có:

$1+q+q^2+q^3+q^4+\dots +q^{k-1}+q^{(k+1)-1}$

$=\frac{1-q^k}{1-q}+q^{(k+1)-1}$$=\frac{1-q^k}{1-q}+q^k$$=\frac{1-q^k+q^k(1-q)}{1-q}$$=\frac{1-q^k+q^k-q^{k+1}}{1-q}$$=\frac{1-q^{k+1}}{1-q}.$

Vậy đẳng thức đúng với n = k + 1.

Theo nguyên lí quy nạp toán học, đẳng thức đúng với mọi số tự nhiên n ≥ 1.