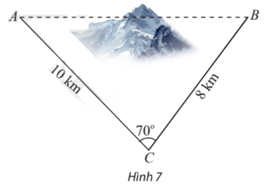
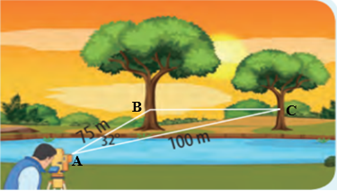
Với số liệu đo được từ một bên bờ sông như hình vẽ bên, bạn hãy giúp nhân viên đo đạc tính khoảng cách giữa hai cái cây bên kia bờ sông.

Với số liệu đo được từ một bên bờ sông như hình vẽ bên, bạn hãy giúp nhân viên đo đạc tính khoảng cách giữa hai cái cây bên kia bờ sông.

Câu hỏi trong đề: Bài tập Giải tam giác và ứng dụng thực tế có đáp án !!
Quảng cáo
Trả lời:
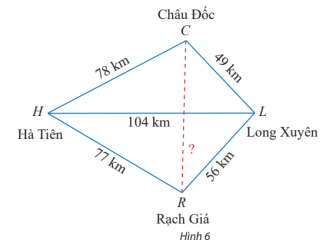
Gọi vị trí của người đo đạc đứng là điểm A và gọi B, C lần lượt là vị trí hai cái cây bên kia sông. Ta có tam giác ABC với AC = 100 m ; AB = 75 m và .
Áp dụng định lí côsin cho tam giác ABC ta có :
BC2 = AB2 + AC2 – 2.AB.AC.cosA = 752 + 1002 – 2.75.100.cos32° ≈ 2 904,3.
⇒ BC ≈ ≈ 53,9 m.
Vậy hai cái cây bên kia sông cách nhau khoảng 53,9 m.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
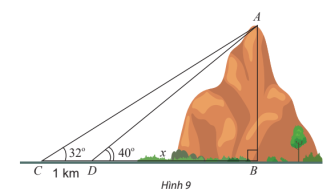
Đặt BD = x km, khi đó ta có CB = BD + CD = x + 1.
Trong tam giác ABC vuông tại B ta có: (1)
Trong tam giác ABD vuông tại B ta có:
(2)
Từ (1) và (2) suy ra:
Suy ra AB = x.tan40° ≈ 2,92.tan40° ≈ 2,45 km.
Vậy chiều cao AB của một ngọn núi khoảng 2,45 km.
Lời giải
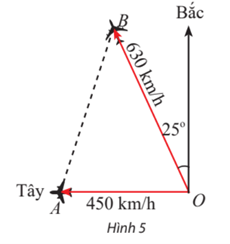
Gọi A và B lần lượt là vị trí của hai máy bay sau khi cất cánh 90 phút.
Đổi 90 phút = 1,5 giờ.
Sau 90 phút (tức là sau 1,5 giờ) chiếc máy bay di chuyển theo hướng tây đi được quãng đường là: 450.1,5 = 675 km, tức là OA = 675 km.
Sau 90 phút (tức là sau 1,5 giờ) chiếc máy bay di chuyển theo hướng lệch bắc 25° về phía tây đi được quãng đường là: 630.1,5 = 945 km, tức là OB = 945 km.
Ta có .
Áp dụng định lí côsin cho tam giác OAB ta có:
AB2 = OA2 + OB2 – 2.OA.OB.cos = 6752 + 9452 – 2.675.945.cos65o ≈ 809 494,8
⇒ AB = .
Vậy sau 90 phút hai máy bay cách nhau khoảng 899,7 km.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.