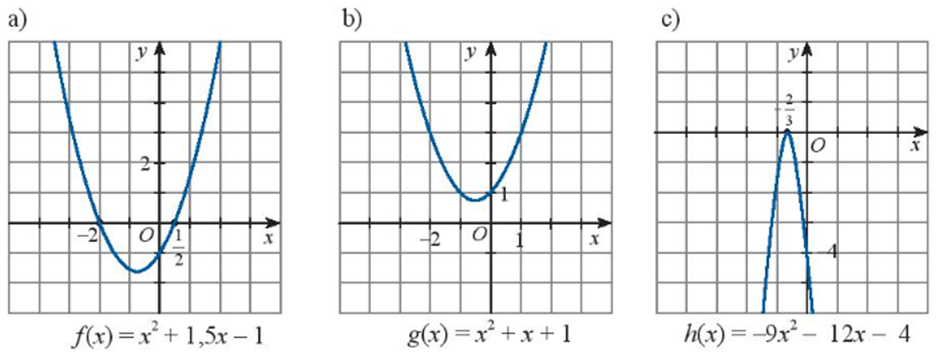
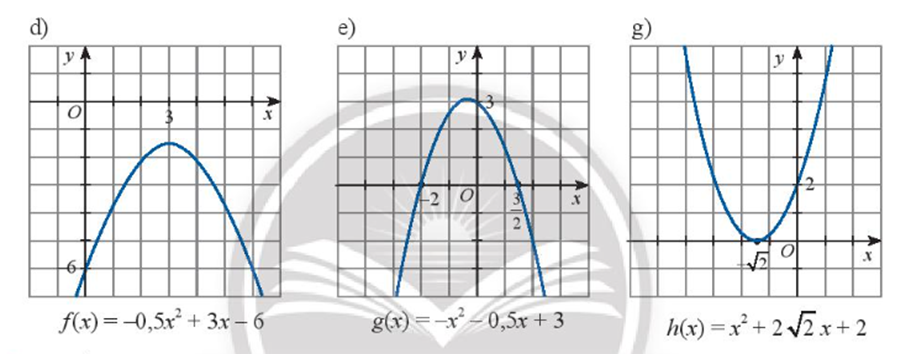
Xét dấu của tam thức bậc hai sau đây:
a) f(x) = 2x2 + 4x + 2;
b) f(x) = - 3x2 + 2x + 21;
c) f(x) = - 2x2 + x – 2;
d) f(x) = -4x(x + 3) – 9;
e) f(x) = (2x + 5)(x – 3).
Xét dấu của tam thức bậc hai sau đây:
a) f(x) = 2x2 + 4x + 2;
b) f(x) = - 3x2 + 2x + 21;
c) f(x) = - 2x2 + x – 2;
d) f(x) = -4x(x + 3) – 9;
e) f(x) = (2x + 5)(x – 3).
Câu hỏi trong đề: Bài tập Toán 10 Bài 1. Dấu của tam thức bậc hai có đáp án !!
Quảng cáo
Trả lời:
a) Tam thức bậc hai f(x) = 2x2 + 4x + 2 có ∆ = 42 – 4.2.2 = 16 – 16 = 0. Do đó f(x) có một nghiệm kép x1 = x2 = - 1 và a = 2 > 0.
Ta có bảng xét dấu sau:
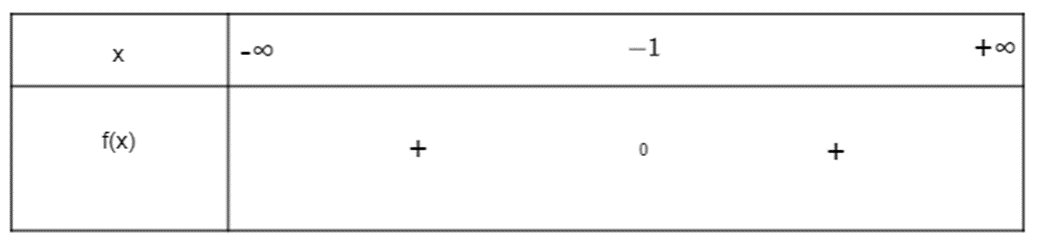
Vậy f(x) = 2x2 + 4x + 2 mang dấu dương khi x ≠ - 1.
b) Tam thức bậc hai f(x) = - 3x2 + 2x + 21 có ∆ = 22 – 4.(-3).21 = 256 > 0. Do đó f(x) có hai nghiệm phân biệt x1 = 3 và x2 = và a = -3 < 0.
Ta có bảng xét dấu:
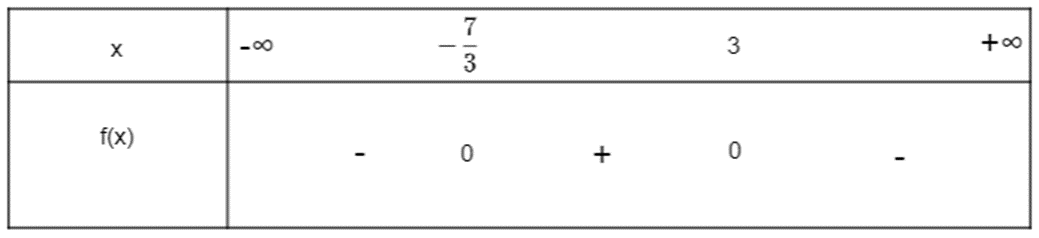
Vậy f(x) = - 3x2 + 2x + 21 dương khi x thuộc khoảng và f(x) = - 3x2 + 2x + 21 âm khi x thuộc hai khoảng và .
c) Tam thức bậc hai f(x) = - 2x2 + x – 2 có ∆ = 12 – 4.(-2).(-2) = 1 – 16 = -15 < 0. Do đó hàm số vô nghiệm và a = -2 < 0.
Ta có bảng xét dấu:
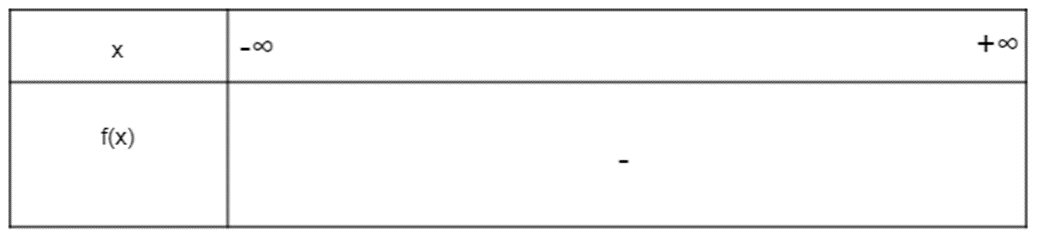
Vậy f(x) = - 2x2 + x – 2 âm với mọi giá trị thực của x.
d) Ta có f(x) = -4x(x + 3) – 9 = - 4x2 – 12x – 9.
Xét tam thức f(x) = - 4x2 – 12x – 9 có ∆ = (-12)2 – 4.(-4)(-9) = 144 – 144 = 0. Do đó f(x) có nghiệm kép x1 = x2 = và a = - 4 < 0.
Ta có bảng xét dấu:
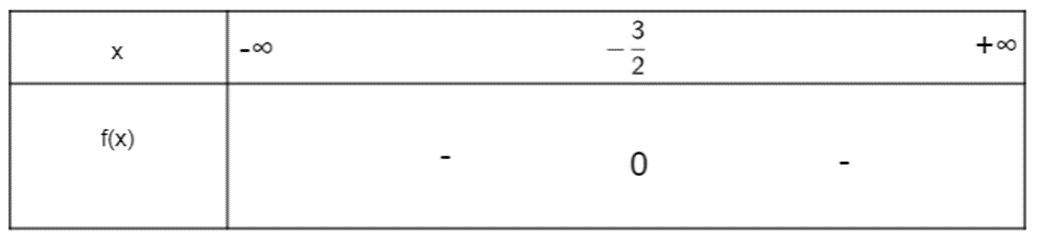
Vậy f(x) mang dấu âm khi x ≠ .
e) Ta có f(x) = (2x + 5)(x – 3) = 2x2 – 6x + 5x – 15 = 2x2 – x – 15.
Tam thức f(x) = 2x2 – x – 15 có ∆ = (-1)2 – 4.2.(-15) = 1 + 120 = 121 > 0. Do đó f(x) có hai nghiệm phân biệt x1 = 3 và x2 = và a = 2 > 0.
Ta có bảng xét dấu:
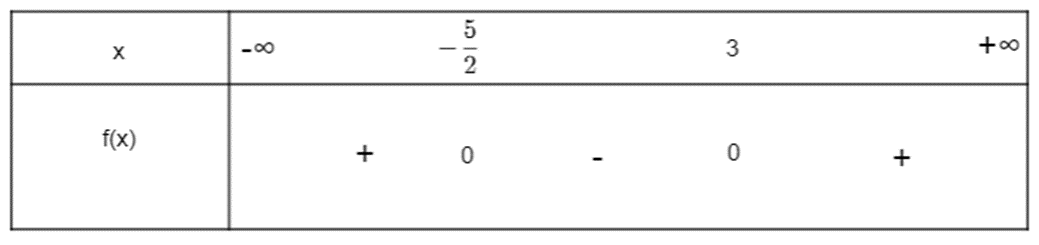
Vậy f(x) = (2x + 5)(x – 3) âm khi x thuộc khoảng và f(x) = (2x + 5)(x – 3) dương khi x thuộc hai khoảng và (3; +∞).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Diện tích khung dây thép hình chữ nhật ban đầu là: 20.15 = 300 (cm2).
Diện tích khung hình chữ nhật mới là: (20 + x)(15 – x) = 300–5x – x2 (cm2).
Xét hiệu f(x) = 300 – 300 + 5x + x2 = x2 + 5x.
Ta có f(x) = x2 – 5x là tam thức bậc hai có ∆ = 52 – 4.1.0 = 25 > 0. Do đó h(x) có hai nghiệm phân biệt x1 = 0, x2 = -5 và a = 1 > 0.
Khi đó ta có bảng xét dấu:
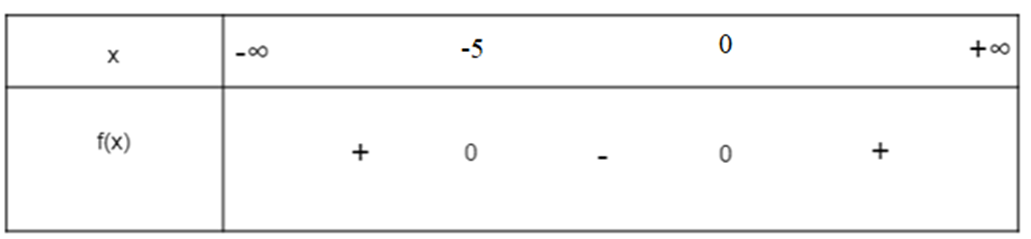
Suy ra f(x) âm khi x thuộc khoảng (-5; 0), f(x) dương khi x thuộc hai khoảng (-∞; -5) và (0; +∞).
Vậy với x thuộc khoảng (-5; 0) thì diện tích của khung dây thép tăng lên, x thuộc hai khoảng (-∞; -5) và (0; +∞) thì diện tích của khung dây thép giảm đi, và x = - 5 hoặc x = 0 thì diện tích khung dây thép không đổi.
Lời giải
Ta có h(x) = -0,1x2 + x – 1 là tam thức bậc hai với a = -0,1, b = 1 và c = -1.
Tam thức bậc hai h(x) = -0,1x2 + x – 1 có ∆ = 12 – 4.(-0,1).(-1) = 0,6 > 0. Do đó h(x) có hai nghiệm phân biệt x1 = 5 + , x2 = 5 – và a = -0,1 < 0.
Ta có bảng xét dấu sau:
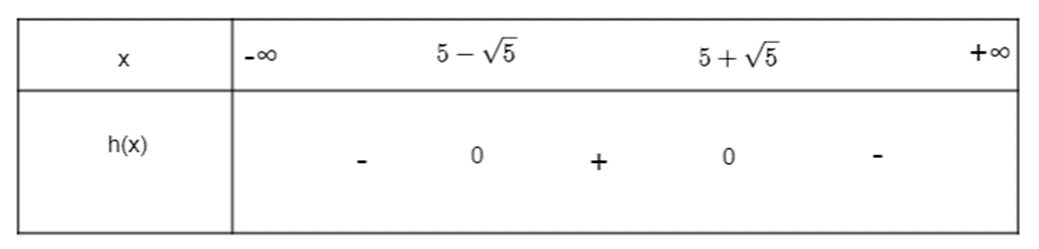
Suy ra h(x) dương khi x thuộc khoảng và h(x) âm khi x thuộc hai khoảng và .
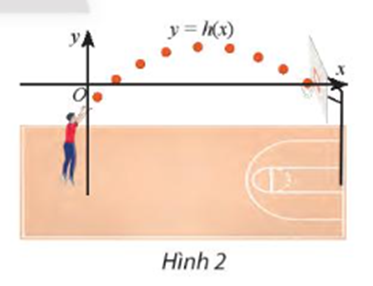
Dựa vào hình vẽ ta thấy trục Ox chính là vành rổ.
Ta có và
Vậy với x thuộc khoảng (1,1; 8,9) thì bóng nằm cao hơn vành rổ và với x thuộc khoảng (– ∞;1,1) và (8,9 ; + ∞) thì bóng nằm thấp hơn vành rổ và với x ≈ 1,1 hoặc x ≈ 8,9 thì bóng nằm ngang vành rổ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.