Hãy khai triển và rút gọn biểu thức

(1 + x)⁴ + (1 – x)⁴.

Sử dụng kết quả đó để tính gần đúng giá trị của biểu thức 1,05⁴ + 0,95⁴.

Mật mã là một dãy số có ba chữ số nên việc thiết lập mật mã chia làm ba giai đoạn:

- Chữ số đầu tiên có 10 cách chọn;

- Chữ số thứ hai có 10 cách chọn;

- Chữ số thứ ba có 10 cách chọn.

Theo quy tắc nhân, ta có: 10.10.10 = 1 000 mật mã.

Vậy có tất cả 1 000 cách chọn mật mã cho khóa.

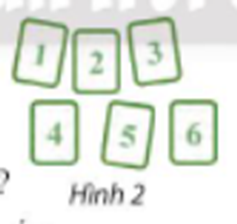
a) Số thành viên của nhóm là 4 + 5 + 6 = 15 (thành viên)

Số cách để nhóm cử ra một thành viên của nhóm tham gia một công việc tình nguyện là tổ hợp chập 1 của 15. Do đó ta có số cách cử một thành viên trong nhóm là:

\(C_{15}^1 = 15\) (cách).

Vậy số cách cử một thành viên trong nhóm là 15 cách.

b) Số cách để nhóm cử ra ba thành viên của nhóm đang học ở ba lớp khác nhau tham gia một công việc tình nguyện là:

\(C_4^1.C_5^1.C_6^1 = 120\)(cách).

Vậy có 120 cách để nhóm cử ra ba thành viên của nhóm đang học ở ba lớp khác nhau tham gia một công việc tình nguyện.

c) Số cách cử ra 2 thành viên của nhóm đang học ở hai lớp khác nhau có thể có 3 phương án khác nhau:

- Phương án 1: 1 thành viên lớp 10A và 1 thành viên lớp 10B, có \(C_4^1.C_5^1 = 20\)(cách).

- Phương án 2: 1 thành viên lớp 10B và 1 thành viên lớp 10C, có \(C_5^1.C_6^1 = 30\)(cách).

- Phương án 3: 1 thành viên lớp 10A và 1 thành viên lớp 10C, có \(C_4^1.C_6^1 = 24\)(cách).

Theo quy tắc cộng, có tất cả 20 + 30 + 24 = 74 cách cử ra 2 thành viên của nhóm đang học ở hai lớp khác nhau tham gia một công việc tình nguyện.