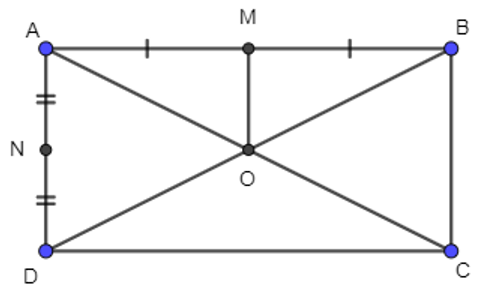
Cho hình chữ nhật ABCD tâm O. Gọi M, N lần lượt là trung điểm của các cạnh AB, AD. Chọn khẳng định đúng trong các khẳng định sau:

+) Xét bất phương trình x – y ≥ – 2

Vẽ đường thẳng d₁: x – y = – 2 ;

Lấy điểm O(0; 0) ∉ d₁ có 0 – 0 = 0 > – 2. Do đó O(0; 0) thuộc vào miền nghiệm của bất phương trình.

Do đó miền nghiệm D₁ là nửa mặt phẳng có bờ là đường thẳng d₁ chứa điểm O và kể cả đường thẳng d₁.

+) Xét bất phương trình x + y ≤ 4

Vẽ đường thẳng d₂: x + y = 4;

Lấy điểm O(0; 0) ∉ d₂ có 0 + 0 = 0 < 4. Do đó O(0; 0) thuộc vào miền nghiệm của bất phương trình.

Do đó miền nghiệm D₂ là nửa mặt phẳng có bờ là đường thẳng d₂ chứa điểm O và kể cả đường thẳng d₂.

+) Xét bất phương trình x – 5y ≤ – 2

Vẽ đường thẳng d₃: x – 5y = – 2;

Lấy điểm O(0; 0) ∉ d₃ có 0 – 5.0 = 0 > – 2. Do đó O(0; 0) không thuộc vào miền nghiệm của bất phương trình.

Do đó miền nghiệm D₃ là nửa mặt phẳng có bờ là đường thẳng d₃ không chứa điểm O và kể cả đường thẳng d₃.

Vậy miền nghiệm của hệ bất phương trình là giao của ba miền nghiệm D₁, D₂ và D₃ là miền trong của tam giác ABC có A(1; 3), B(3; 1), C(– 2; 0).

Giá trị nhỏ nhất của biểu thức F(x; y) đạt được trên các đỉnh của tam giác ABC.

Ta có:

Tại điểm A(1; 3) ta có: F(x; y) = – 2.1 + 3 = 1.

Tại điểm B(3; 1) ta có: F(x; y) = – 2.3 + 1 = – 5.

Tại điểm C(– 2; 0) ta có: F(x; y) = – 2.(– 2) + 0 = 4.

Vậy giá trị nhỏ nhất của F(x; y) = – 5.

Đáp án đúng là: B

Ta có mệnh đề phủ định của mệnh đề “Phương trình ax² + bx + c = 0 (a ≠ 0) vô nghiệm” là: Phương trình ax² + bx + c = 0 (a ≠ 0) có nghiệm.