Một mảnh vườn hình thoi có tổng độ dài hai đường chéo \[120cm\]. Tính diện tích mảnh vườn hình thoi; biết rằng đường chéo thứ nhất bằng một nửa độ dài đường chéo thứ hai.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Vì đường chéo thứ nhất bằng một nửa đường chéo thứ hai hay đường chéo thứ hai gấp đôi đường chéo thứ nhất.
Tổng số phần bằng nhau là \(2 + 1 = 3\) (phần).
Độ dài đường chéo thứ nhất là \(120:3.1 = 40\left( {cm} \right)\).
Độ dài đường chéo thứ hai là \(120:3.2 = 80\left( {cm} \right)\).
Diện tích mảnh vườn hình thoi là \(\frac{1}{2} \cdot 40 \cdot 80 = 1600\left( {c{m^2}} \right)\)
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
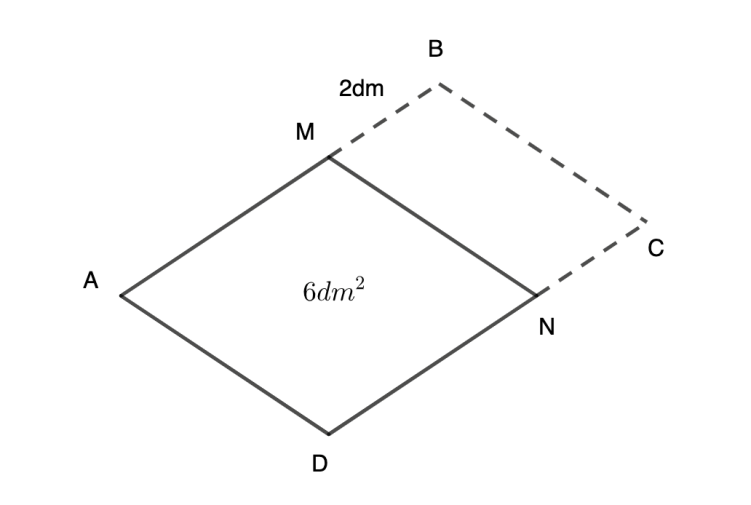
\[AMND\] là hình thoi nên \[AM = MN = DN = AD\]
\[ABCD\]là hình bình hành nên \[BC = AD\]
\[ \Rightarrow AM = BC = DN = AD\]
Chu vi hình bình hành là:
\[AM + BC + DN + AD + MB + NC = 4DN + 2MB = 2m = 20dm\]
\[ \Rightarrow 4DN + 2.2 = 20 \Rightarrow {\rm{4DN = 16}} \Rightarrow {\rm{DN = 4(dm)}}\]
Gọi h là độ dài đường cao của hình thoi AMND kẻ từ điểm M xuống cạnh DN
\[h = {S_{AMND}}:DN = 6:4 = 1,5(dm)\]
h đồng thời là độ dài đường cao của hình bình hành ABCD
Diện tích hình bình hành là: \[{S_{ABCD}} = CD.h = \left( {4 + 2} \right).1,5 = 9(d{m^2})\]
Lời giải
Lời giải
Độ dài đường chéo lớn là \[220:\left( {2 + 3} \right).3 = 132{\rm{ }}\left( m \right)\]
Độ dài đường chéo nhỏ là \[220 - 132{\rm{ = 88}}\left( m \right)\]
Diện tích mảnh vườn là \[\frac{1}{2} \cdot 132 \cdot 88 = 5808\left( {{m^2}} \right)\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo