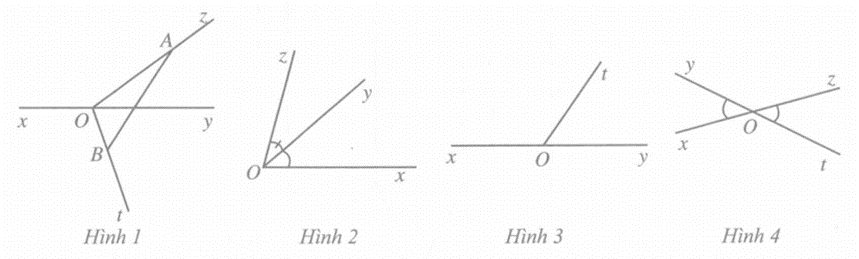
- Ở Hình 1, với điểm A bất kì trên tia Oz (A khác…), điểm B bất kì trên tia Ot (B khác …) thì đoạn thẳng AB luôn cắt ……………………… xy. Khi đó, hai tia Oz, Ot gọi là ……………………………………… đường thẳng xy.
- Ở Hình 2, hai góc xOy và zOy có O là ………………, tia Oy là ……………… và hai cạnh Ox, Oz nằm về …………………………………… cạnh chung Oy. Hai góc xOy và zOy như thế gọi là ………………………………………………………………………..
- Cho góc xOz (khác góc bẹt) và tia Oy nằm trong góc đó, tức là mỗi điểm M (M khác ...) của tia … đều là ……………………… của góc xOz. Khi đó, hai góc xOy và yOz là ……………………………………… và …………... = ……………+ ……………
- Nếu góc xOz là góc bẹt thì với mỗi tia Oy (khác hai tia Ox,….) , ta cũng có:
………….. = ………….. + …………….
- Hai góc bù nhau là hai góc …………………………………… 180°.
- Hai góc vừa ……………vừa ……………………………. kề bù (chẳng hạn, hai góc xOt và yOt ở Hình 3 là ……………………).
- Hai góc có một cạnh ……………., hai cạnh còn lại ………………………….. là ………………. kề bù.
- Hai góc đối đỉnh là …………………………………………………. của góc kia (chẳng hạn, hai góc xOy và zOt ở Hình 4 là ……………………………).
- Hai góc đối đỉnh thì ……….. nhau.

- Ở Hình 1, với điểm A bất kì trên tia Oz (A khác…), điểm B bất kì trên tia Ot (B khác …) thì đoạn thẳng AB luôn cắt ……………………… xy. Khi đó, hai tia Oz, Ot gọi là ……………………………………… đường thẳng xy.
- Ở Hình 2, hai góc xOy và zOy có O là ………………, tia Oy là ……………… và hai cạnh Ox, Oz nằm về …………………………………… cạnh chung Oy. Hai góc xOy và zOy như thế gọi là ………………………………………………………………………..
- Cho góc xOz (khác góc bẹt) và tia Oy nằm trong góc đó, tức là mỗi điểm M (M khác ...) của tia … đều là ……………………… của góc xOz. Khi đó, hai góc xOy và yOz là ……………………………………… và …………... = ……………+ ……………
- Nếu góc xOz là góc bẹt thì với mỗi tia Oy (khác hai tia Ox,….) , ta cũng có:
………….. = ………….. + …………….
- Hai góc bù nhau là hai góc …………………………………… 180°.
- Hai góc vừa ……………vừa ……………………………. kề bù (chẳng hạn, hai góc xOt và yOt ở Hình 3 là ……………………).
- Hai góc có một cạnh ……………., hai cạnh còn lại ………………………….. là ………………. kề bù.
- Hai góc đối đỉnh là …………………………………………………. của góc kia (chẳng hạn, hai góc xOy và zOt ở Hình 4 là ……………………………).
- Hai góc đối đỉnh thì ……….. nhau.
Quảng cáo
Trả lời:
- Ở Hình 1, với điểm A bất kì trên tia Oz (A khác O), điểm B bất kì trên tia Ot (B khác O) thì đoạn thẳng AB luôn cắt đường thẳng xy. Khi đó, hai tia Oz, Ot gọi là nằm về hai phía của đường thẳng xy.
- Ở Hình 2, hai góc xOy và zOy có O là đỉnh chung, tia Oy là cạnh chung và hai cạnh Ox, Oz nằm về hai phía của cạnh chung Oy. Hai góc xOy và zOy như thế gọi là hai góc kề nhau.
- Cho góc xOz (khác góc bẹt) và tia Oy nằm trong góc đó, tức là mỗi điểm M (M khác O) của tia Oy đều là điểm trong của góc xOz. Khi đó, hai góc xOy và yOz là hai góc kề nhau và .
- Nếu góc xOz là góc bẹt thì với mỗi tia Oy (khác hai tia Ox, Oz) , ta cũng có:
.
- Hai góc bù nhau là hai góc có tổng số đo bằng 180°.
- Hai góc vừa kề nhau vừa bù nhau gọi là hai góc kề bù (chẳng hạn, hai góc xOt và yOt ở Hình 3 là hai góc kề bù).
- Hai góc có một cạnh chung, hai cạnh còn lại là hai tia đối là hai góc kề bù.
- Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia (chẳng hạn, hai góc xOy và zOt ở Hình 4 là hai góc đối đỉnh).
- Hai góc đối đỉnh thì bằng nhau.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
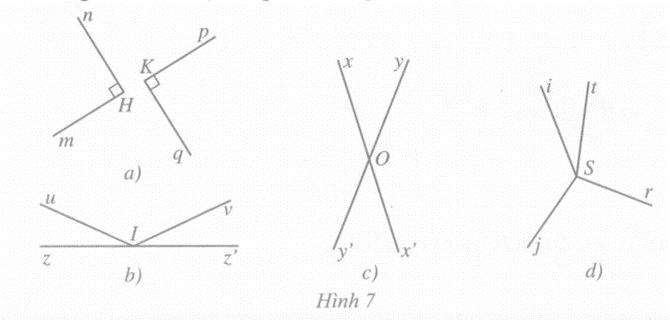
Ở Hình 7, chỉ có trường hợp Hình 7c là có hai góc đối đỉnh (khác góc bẹt và góc không), cụ thể các cặp góc đối đỉnh đó là: xOy và y’Ox’, yOx’ và y’Ox.
Lời giải
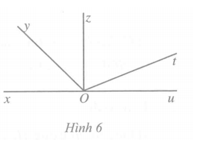
Ở hình 6, các cặp góc kề bù (khác góc bẹt) là: uOt và tOx, uOz và zOx, uOy và xOy.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.