Giải SBT Toán 7 Bài 4. Định lí có đáp án
33 người thi tuần này 4.6 1.5 K lượt thi 11 câu hỏi
🔥 Đề thi HOT:
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 1
20.4 K lượt thi
17 câu hỏi
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 04
7.2 K lượt thi
30 câu hỏi
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
15 K lượt thi
15 câu hỏi
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 2
15.7 K lượt thi
17 câu hỏi
Bộ 7 đề thi học kì 2 Toán 7 Cánh Diều có đáp án - Đề 01
5.6 K lượt thi
23 câu hỏi
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 3
15.4 K lượt thi
29 câu hỏi
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 01
5.6 K lượt thi
21 câu hỏi
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 4
15 K lượt thi
29 câu hỏi
Nội dung liên quan:
Danh sách câu hỏi:
Câu 1
Cho định lí: “Nếu Am, Bn là hai tia phân giác của hai góc trong cùng phía tạo bởi một đường thẳng cắt hai đường thẳng song song thì Am vuông góc với Bn”.
a) Vẽ hình minh hoạ nội dung định lí trên.
Cho định lí: “Nếu Am, Bn là hai tia phân giác của hai góc trong cùng phía tạo bởi một đường thẳng cắt hai đường thẳng song song thì Am vuông góc với Bn”.
a) Vẽ hình minh hoạ nội dung định lí trên.
Lời giải
Câu 2
Cho định lí: “Nếu Am, Bn là hai tia phân giác của hai góc trong cùng phía tạo bởi một đường thẳng cắt hai đường thẳng song song thì Am vuông góc với Bn”.
b) Viết giả thiết, kết luận của định lí trên.
Cho định lí: “Nếu Am, Bn là hai tia phân giác của hai góc trong cùng phía tạo bởi một đường thẳng cắt hai đường thẳng song song thì Am vuông góc với Bn”.
b) Viết giả thiết, kết luận của định lí trên.
Lời giải
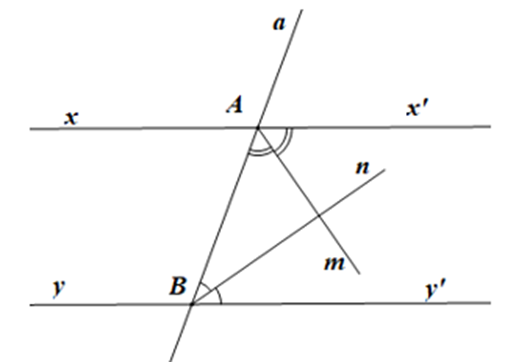
b) Viết giả thiết và kết luận của định lí:
|
GT |
xx’ // yy’, a cắt xx’ tại A, a cắt yy’ tại B, Am, Bn lần lượt là tia phân giác của |
|
KL |
Am ⊥ Bn. |
Câu 3
Vẽ hình minh hoạ và viết giả thiết, kết luận của mỗi định lí sau:
a) Nếu một đường thẳng cắt một trong hai đường thẳng song song thì nó cắt đường thẳng còn lại;
Vẽ hình minh hoạ và viết giả thiết, kết luận của mỗi định lí sau:
a) Nếu một đường thẳng cắt một trong hai đường thẳng song song thì nó cắt đường thẳng còn lại;
Lời giải
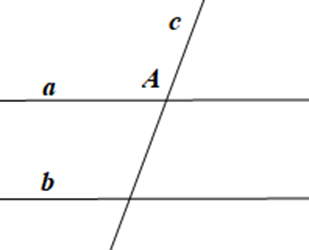
Viết giả thiết và kết luận của định lí:
|
GT |
a // b, c cắt a tại A |
|
KL |
c, b cắt nhau. |
Câu 4
Vẽ hình minh hoạ và viết giả thiết, kết luận của mỗi định lí sau:
b) Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại;
Vẽ hình minh hoạ và viết giả thiết, kết luận của mỗi định lí sau:
b) Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại;
Lời giải
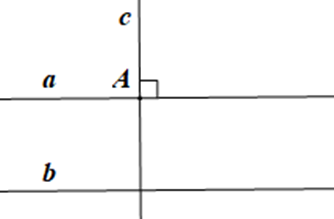
Viết giả thiết và kết luận của định lí:
|
GT |
a // b, c ⊥ a tại A. |
|
KL |
c ⊥ b. |
Câu 5
Vẽ hình minh hoạ và viết giả thiết, kết luận của mỗi định lí sau:
c) Nếu hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song với nhau.
Vẽ hình minh hoạ và viết giả thiết, kết luận của mỗi định lí sau:
c) Nếu hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song với nhau.
Lời giải
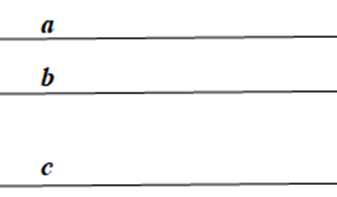
Viết giả thiết và kết luận của định lí:
|
GT |
a // b, a // c. |
|
KL |
b // c. |
Câu 6
Vẽ hình minh hoạ và viết giả thiết, kết luận của mỗi định lí sau:
a) Nếu hai góc nhọn xOy và mIn có Ox // Im, Oy // In thì hai góc đó bằng nhau;
Vẽ hình minh hoạ và viết giả thiết, kết luận của mỗi định lí sau:
a) Nếu hai góc nhọn xOy và mIn có Ox // Im, Oy // In thì hai góc đó bằng nhau;
Lời giải
Viết giả thiết và kết luận của định lí:
|
GT |
là góc nhọn, Ox // Im, Oy // In. |
|
KL |
|
Câu 7
Vẽ hình minh hoạ và viết giả thiết, kết luận của mỗi định lí sau:
b) Nếu hai góc tù xOy và mIn có Ox // Im, Oy // In thì hai góc đó bằng nhau;
Vẽ hình minh hoạ và viết giả thiết, kết luận của mỗi định lí sau:
b) Nếu hai góc tù xOy và mIn có Ox // Im, Oy // In thì hai góc đó bằng nhau;
Lời giải
Viết giả thiết và kết luận của định lí:
|
GT |
là góc tù, Ox // Im, Oy // In. |
|
KL |
|
Câu 8
Vẽ hình minh hoạ và viết giả thiết, kết luận của mỗi định lí sau:
c) Nếu góc xOy nhọn, góc mIn tù có Ox // Im, Oy // In thì hai góc đó bù nhau.
Vẽ hình minh hoạ và viết giả thiết, kết luận của mỗi định lí sau:
c) Nếu góc xOy nhọn, góc mIn tù có Ox // Im, Oy // In thì hai góc đó bù nhau.
Lời giải
Viết giả thiết và kết luận của định lí:
|
GT |
là góc nhọn, là góc tù, Ox // Im, Oy // In. |
|
KL |
|
Câu 9
Cho định lí: “Nếu hai đường thẳng xx’, yy’ cắt nhau tại O và góc xOy là góc vuông thì các góc x’Oy, x’Oy’, xOy’ cũng là góc vuông”.
a) Vẽ hình minh hoạ nội dung định lí trên.
Cho định lí: “Nếu hai đường thẳng xx’, yy’ cắt nhau tại O và góc xOy là góc vuông thì các góc x’Oy, x’Oy’, xOy’ cũng là góc vuông”.
a) Vẽ hình minh hoạ nội dung định lí trên.
Lời giải
Câu 10
Cho định lí: “Nếu hai đường thẳng xx’, yy’ cắt nhau tại O và góc xOy là góc vuông thì các góc x’Oy, x’Oy’, xOy’ cũng là góc vuông”.
b) Viết giả thiết, kết luận của định lí trên.
Cho định lí: “Nếu hai đường thẳng xx’, yy’ cắt nhau tại O và góc xOy là góc vuông thì các góc x’Oy, x’Oy’, xOy’ cũng là góc vuông”.
b) Viết giả thiết, kết luận của định lí trên.
Lời giải
b) Viết giả thiết và kết luận của định lí:
|
GT |
xx’, yy’ cắt nhau tại O,
|
|
KL |
|
Câu 11
Cho định lí: “Nếu hai đường thẳng xx’, yy’ cắt nhau tại O và góc xOy là góc vuông thì các góc x’Oy, x’Oy’, xOy’ cũng là góc vuông”.
c) Chứng minh định lí trên.
Cho định lí: “Nếu hai đường thẳng xx’, yy’ cắt nhau tại O và góc xOy là góc vuông thì các góc x’Oy, x’Oy’, xOy’ cũng là góc vuông”.
c) Chứng minh định lí trên.
Lời giải
Ta có: (hai góc kề bù)
Suy ra
Mà (các cặp góc đối đỉnh)
Do đó
Vậy
4.6
298 Đánh giá
50%
40%
0%
0%
0%