1. Lớp 7
  2. Toán
  3. Giải VBT Toán 7 Cánh diều Bài tập cuối chương 4 có đáp án

Giải VBT Toán 7 Cánh diều Bài tập cuối chương 4 có đáp án

26 người thi tuần này 4.6 1.7 K lượt thi 20 câu hỏi

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

🔥 Học sinh cũng đã học

11 người thi tuần này

Đề thi Cuối kì 2 Toán 7 trường THCS Đông Xuân (Hà Nội) năm 2022-2023 có đáp án

22 lượt thi x câu hỏi
11 người thi tuần này

Đề thi Cuối kì 2 Toán 7 Phòng GD&ĐT Tây Hồ (Hà Nội) năm 2023-2024 có đáp án

22 lượt thi x câu hỏi
12 người thi tuần này

Đề thi Cuối kì 2 Toán 7 trường THCS Phan Chu Trinh (Hà Nội) năm 2024-2025 có đáp án

24 lượt thi x câu hỏi

Bộ 5 đề thi giữa kì 1 Toán 7 Chân trời sáng tạo (2023-2024) có đáp án - Đề 3

0 lượt thi 12 câu hỏi

Bộ 5 đề thi giữa kì 1 Toán 7 Chân trời sáng tạo (2023-2024) có đáp án - Đề 2

0 lượt thi 19 câu hỏi

Bộ 5 đề thi giữa kì 1 Toán 7 Chân trời sáng tạo (2023-2024) có đáp án - Đề 1

0 lượt thi 13 câu hỏi
109 người thi tuần này

Bộ 5 đề thi giữa kì 1 Toán 7 Cánh Diều (2023-2024) có đáp án - Đề 5

451 lượt thi 17 câu hỏi
69 người thi tuần này

Bộ 5 đề thi giữa kì 1 Toán 7 Cánh Diều (2023-2024) có đáp án - Đề 4

411 lượt thi 17 câu hỏi

Danh sách câu hỏi:

Câu 1/20

Cho một ví dụ về hai góc kề nhau, hai góc kề bù, hai góc đối đỉnh.

Lời giải

Cho một ví dụ về hai góc kề nhau, hai góc kề bù, hai góc đối đỉnh (ảnh 1)

Câu 2/20

Thế nào là tia phân giác của một góc ?

Lời giải

Tia phân giác của một góc là tia nằm trong góc và tạo với hai cạnh của góc đó hai góc bằng nhau.

Câu 3/20

Cho một ví dụ về hai góc đồng vị, hai góc so le trong.

Lời giải

Ở Hình 39, ta có:
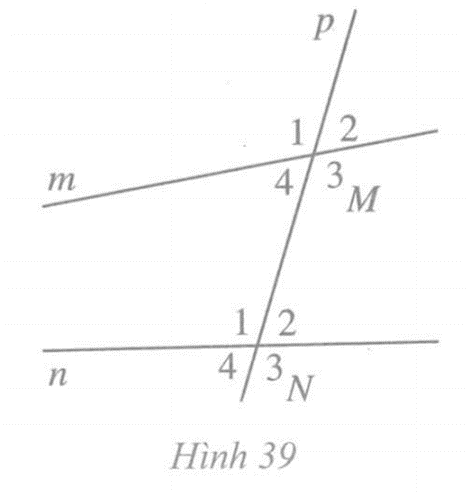
Cho một ví dụ về hai góc đồng vị, hai góc so le trong (ảnh 1)

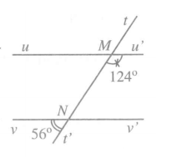
Hai góc M1 và N1 là hai góc đồng vị;

- Hai góc M4 và N2 là hai góc so le trong.

 

Câu 4/20

Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị có bằng nhau hay không ? Hai góc so le trong có bằng nhau hay không ?

Lời giải

Nếu một đường thẳng cắt hai đường thẳng song song thì:

- Hai góc đồng vị bằng nhau.

- Hai góc so le trong bằng nhau.

Câu 5/20

Phát biểu tiên đề Euclid về đường thẳng song song.

Lời giải

Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.

Câu 6/20

Hai góc có tổng số đo bằng 180° có phải là hai góc kề bù hay không ?

Lời giải

Hai góc có tổng số đo bằng 180 độ có phải là hai góc kề bù hay không (ảnh 1)

Ở Hình 40, hai góc nHm và pKq đều là góc vuông, do đó, chúng có tổng số đo bằng 180° nhưng hai góc đó không phải là hai góc kề bù.

Vậy hai góc có tổng số đo bằng 180° chưa chắc đã là hai góc kề bù.

Câu 7/20

Hai góc bằng nhau và có chung đỉnh có phải là hai góc đối đỉnh hay không?

Lời giải

Ở Hình 41, hai góc xOy và uOv bằng nhau (cùng bằng 90°) và có chung đỉnh nhưng hai góc đó không phải hai góc đối đỉnh.

Vậy hai góc bằng nhau và có chung đỉnh chưa chắc đã là hai góc đối đỉnh.

Câu 8/20

Tìm cặp đường thẳng song song trong hình 42a và giải thích vì sao.

Tìm cặp đường thẳng song song trong mỗi hình 42a, 42b, 42c, 42d và giải thích (ảnh 1)

Lời giải

Do ở Hình 42a có cặp góc so le trong là \(\widehat {zAB} = \widehat {ABt'}\) (cùng bằng 124°) nên hai đường thẳng tt’ và zz’ song song với nhau.

Câu 9/20

Tìm cặp đường thẳng song song trong mỗi hình 42a và giải thích vì sao.

Tìm cặp đường thẳng song song trong mỗi hình 42a và giải thích vì sao. (ảnh 1)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 10/20

Tìm cặp đường thẳng song song trong mỗi hình 42c và giải thích vì sao.

Tìm cặp đường thẳng song song trong mỗi hình 42c và giải thích vì sao (ảnh 1)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 11/20

Tìm cặp đường thẳng song song trong mỗi hình 42d và giải thích vì sao.

Tìm cặp đường thẳng song song trong mỗi hình 42d và giải thích vì sao. (ảnh 1)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 12/20

Quan sát Hình 43, trong đó Cx song song với AB, đường thẳng BC cắt đường thẳng DE tại F.

Quan sát Hình 43, Tính số đo góc BCx (ảnh 1)

Tính số đo góc BCx.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 13/20

Quan sát Hình 43, trong đó Cx song song với AB, đường thẳng BC cắt đường thẳng DE tại F.

Quan sát Hình 43, Chứng minh rằng Cx song song với DE. (ảnh 1)

Chứng minh rằng Cx song song với DE.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 14/20

Quan sát Hình 43, trong đó Cx song song với AB, đường thẳng BC cắt đường thẳng DE tại F.

Quan sát Hình 43, Tính số đo góc BCD. (ảnh 1)

Tính số đo góc BCD.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 15/20

Quan sát Hình 44, có mq // xt.

Quan sát Hình 44, có mq // xt. Kể tên các cặp góc đồng vị bằng nhau. (ảnh 1)

Kể tên các cặp góc đồng vị bằng nhau.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 16/20

Quan sát Hình 44, có mq // xt.

Quan sát Hình 44, có mq // xt. Tìm số đo các góc BAC, CDE. (ảnh 1)

Tìm số đo các góc BAC, CDE.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 17/20

Quan sát Hình 44, có mq // xt.

Bạn Nam cho rằng: Nếu quan điểm C ta có thể kẻ được một đường thẳng song song với hai đường thẳng mq và xt thì sẽ tính được \(\widehat {BCE} = 82^\circ \).

Theo em, bạn Nam nói đúng hay sai ? Vì sao ?

Giả sử qua điểm C ta kẻ được đường thẳng uv song song với cả hai đường thẳng mq và (ảnh 1)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 18/20

Quan sát Hình 46.

Quan sát Hình 46. Hai đường thẳng MN và QR có song song với nhau hay không (ảnh 1)
Hai đường thẳng MN và QR có song song với nhau hay không ? Vì sao ?

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 19/20

Quan sát Hình 46.

Quan sát Hình 46. Đường thẳng MN có vuông góc với đường MR hay không (ảnh 1)

Đường thẳng MN có vuông góc với đường MR hay không ? Vì sao ?

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 20/20

Cho hai đường thẳng song song với nhau là xy và mn. Trên đường thẳng xy lấy điểm A, còn trên đường thẳng mn lấy hai điểm B, C phân biệt (Hình 48). Tổng số đo các góc ABC, BCA, CAB bằng bao nhiêu độ ?

Cho hai đường thẳng song song với nhau là xy và mn. Trên đường thẳng xy lấy điểm A (ảnh 1)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem tiếp với tài khoản VIP

Còn 12/20 câu hỏi, đáp án và lời giải chi tiết.

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Đăng ký

Bạn đã có tài khoản?

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack72. All Rights Reserved.
zalo Nhắn tin Zalo Hỏi bài tập