Câu hỏi:
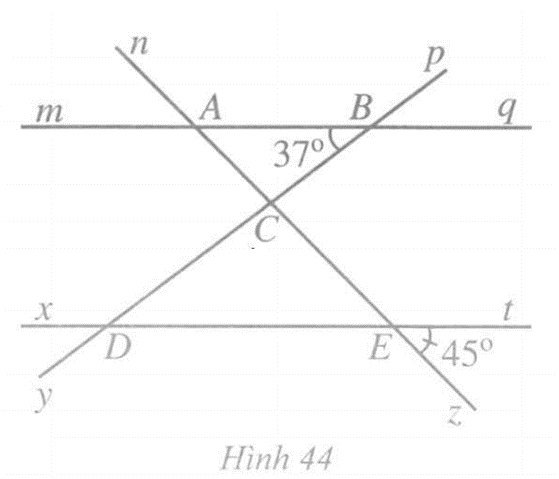
24/10/2022 367Quan sát Hình 44, có mq // xt.
Bạn Nam cho rằng: Nếu quan điểm C ta có thể kẻ được một đường thẳng song song với hai đường thẳng mq và xt thì sẽ tính được \(\widehat {BCE} = 82^\circ \).
Theo em, bạn Nam nói đúng hay sai ? Vì sao ?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Giả sử qua điểm C ta kẻ được đường thẳng uv song song với cả hai đường thẳng mq và xt (Hình 45).
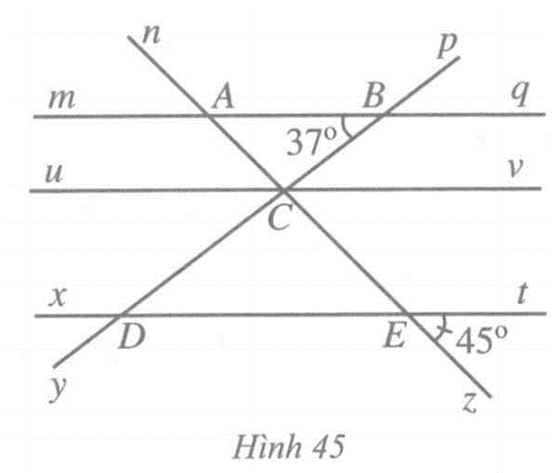
Do mq // uv nên \(\widehat {ABC} = \widehat {BCv}\) (hai góc so le trong)
Mà \(\widehat {ABC} = 37^\circ \) nên \(\widehat {BCv} = 37^\circ \).
Do xt // uv nên \(\widehat {vCE} = \widehat {tEz}\) (hai góc đồng vị)
Mà \(\widehat {tEz} = 45^\circ \) nên \(\widehat {vCE} = 45^\circ \)
Do \(\widehat {BCv}\) và \(\widehat {vCE}\) là hai góc kề nhau nên \(\widehat {BCE} = \widehat {BCv} + \widehat {vCE}\)
Từ đó \(\widehat {BCE} = 37^\circ + 45^\circ = 82^\circ \). Vậy bạn Nam nói đúng.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ở Hình 39, ta có:
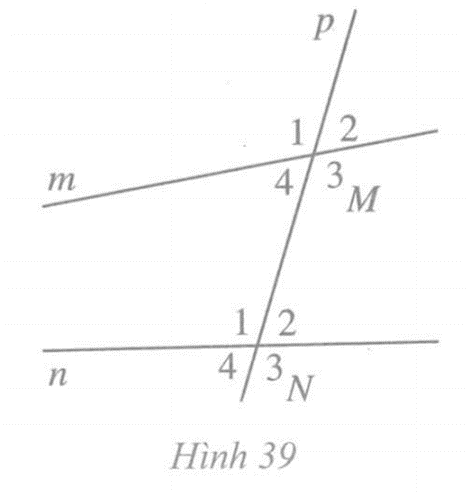
Hai góc M1 và N1 là hai góc đồng vị;
- Hai góc M4 và N2 là hai góc so le trong.
Lời giải
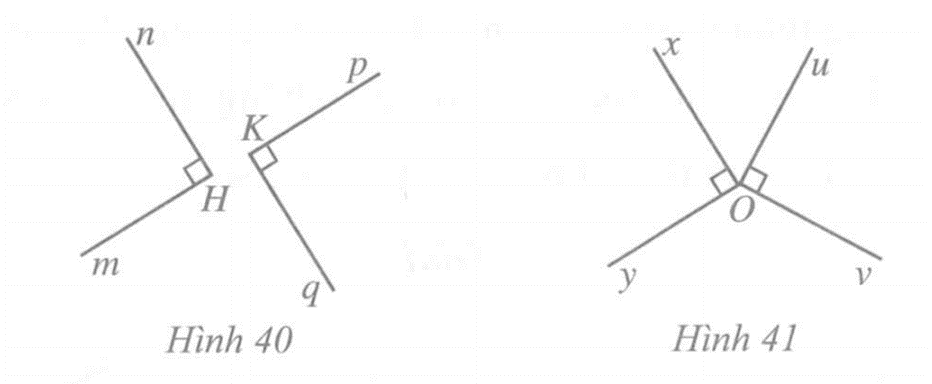
Ở Hình 40, hai góc nHm và pKq đều là góc vuông, do đó, chúng có tổng số đo bằng 180° nhưng hai góc đó không phải là hai góc kề bù.
Vậy hai góc có tổng số đo bằng 180° chưa chắc đã là hai góc kề bù.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo