Giải VBT Toán 7 Cánh diều Bài 13. Tính chất ba đường cao của tam giác có đáp án
48 người thi tuần này 4.6 1.5 K lượt thi 16 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 5 đề thi giữa kì 2 Toán 7 Kết nối tri thức (2022-2023) có đáp án - Đề 5
Bộ 5 đề thi giữa kì 2 Toán 7 Kết nối tri thức (2022-2023) có đáp án - Đề 4
Bộ 5 đề thi giữa kì 2 Toán 7 Kết nối tri thức (2022-2023) có đáp án - Đề 3
Bộ 5 đề thi giữa kì 2 Toán 7 Kết nối tri thức (2022-2023) có đáp án - Đề 2
Bộ 5 đề thi giữa kì 2 Toán 7 Kết nối tri thức (2022-2023) có đáp án - Đề 1
Bộ 10 đề thi giữa kì 2 Toán 7 Chân trời sáng tạo có đáp án - Đề 10
Bộ 10 đề thi giữa kì 2 Toán 7 Chân trời sáng tạo có đáp án - Đề 09
Bộ 10 đề thi giữa kì 2 Toán 7 Chân trời sáng tạo có đáp án - Đề 08
Danh sách câu hỏi:
Lời giải
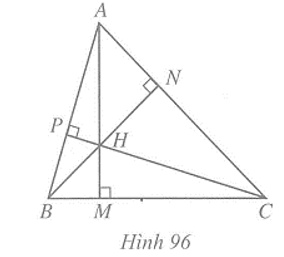
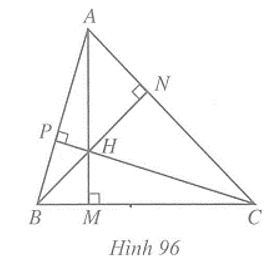
Trong một tam giác đoạn vuông góc kẻ từ một đỉnh đến đường thẳng chứa cạnh đối diện gọi mà một đường cao của tam giác đó (Hình 96).
Lời giải
- Trong một tam giác, ba đường cao đi qua một điểm. Điểm đó được gọi là trực tâm của tam giác (Hình 96)
Lời giải
Đoạn thẳng BA là đường cao đi qua B của tam giác ABC vì B là đỉnh của tam giác và BA vuông góc với AC.
Đoạn thẳng CA là đường cao đi qua C của tam giác ABC vì C là đỉnh của tam giác và CA vuông góc với AB.
Lời giải
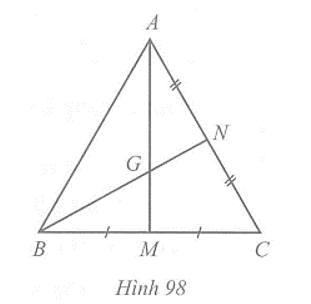
Vẽ AM và BN là hai đường trung tuyến của tam giác ABC.
Vì tam giác ABC đều nên AB = AC, suy ra A thuộc đường trung trực của cạnh BC
Vì MB = MC nên M cũng thuộc đường trung trực của cạnh BC.
Do đó AM là đường trung trực của cạnh BC
Suy ra AM BC hay AM là đường cao của tam giác ABC
Chứng minh tương tự ta cũng có BN là đường cao của tam giác ABC.
Vì hai đường cao AM và BN cắt nhau tại G nên G là trực tâm của tam giác ABC.
Lời giải
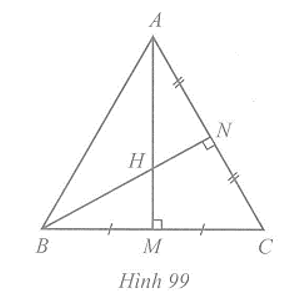
Vẽ AM và BN là hai đường trung tuyến của tam giác ABC.
Vì tam giác ABC có trực tâm H cũng là trọng tâm nên H là giao điểm của AM và BN.
Suy ra AM BC
Do M là trung điểm của BC và AM BC nên AM là đường trung trực của BC suy ra AB = AC.
Chứng minh tương tự ta có BA = BC.
Do đó AB = AC = BC. Vậy tam giác ABC là tam giác đều.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.