✕

✨ Đăng kí VIP để truy cập không giới hạn. Đăng ký ngay

Câu hỏi:

11/07/2024 1,436

Tìm hai góc kề nhau, hai góc kề bù, hai góc đối đỉnh (không tính góc không và góc bẹt)

Xem lời giải

Câu hỏi trong đề: Giải VBT Toán 7 Cánh diều Bài 1. Góc ở vị trí đặc biệt có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

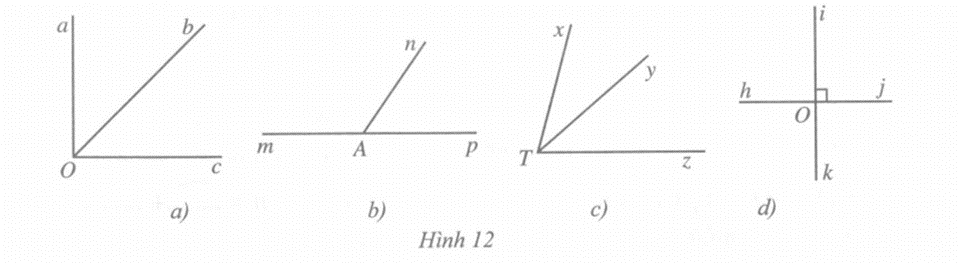
* Ở Hình 12a, cặp góc kề nhau là: aOb và cOb.

Ở Hình 12b, cặp góc kề nhau là: mAn và pAn.

Ở Hình 12c, cặp góc kề nhau là: xTy và zTy.

Ở Hình 12d, các cặp góc kề nhau là: hOi và iOj, hOi và hOk, iOj và jOk, jOk và kOh.

* Ở Hình 12a và Hình 12c không có cặp góc kề bù nào.

Ở Hình 12b có cặp góc kề bù (khác góc bẹt) là: mAn và pAn.

Ở Hình 12d có các cặp góc kề bù (khác góc bẹt) là: hOi và iOj, hOi và hOk, iOj và jOk, jOk và hOk.

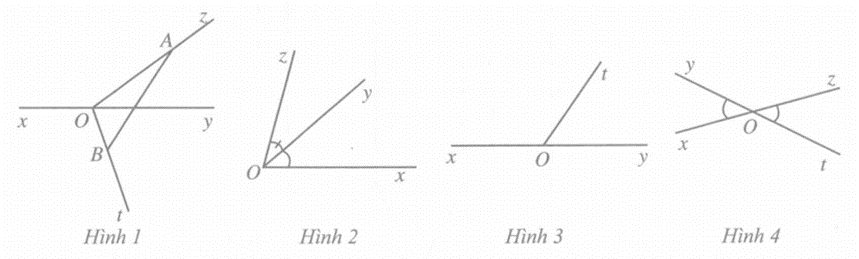
* Ở các hình 12a, 12b, 12c không có cặp góc đối đỉnh nào. Ở Hình 12d có các cặp góc đối đỉnh là: hOi và jOk, iOj và hOk.

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Tìm hai góc đối đỉnh (khác góc bẹt và góc không) trong mỗi hình 7a, 7b, 7c, 7d:

Xem đáp án

Lời giải

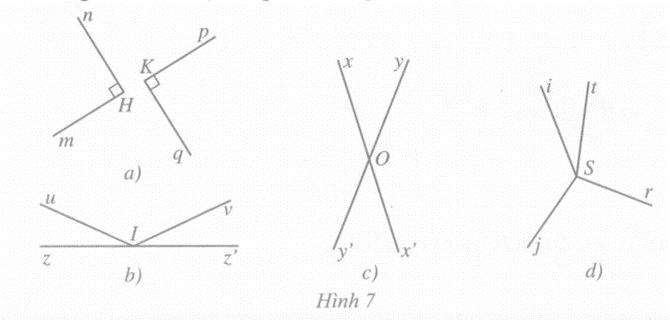
Ở Hình 7, chỉ có trường hợp Hình 7c là có hai góc đối đỉnh (khác góc bẹt và góc không), cụ thể các cặp góc đối đỉnh đó là: xOy và y’Ox’, yOx’ và y’Ox.

Câu 2

Tìm các cặp góc kề bù (khác góc bẹt) ở Hình 6.

Xem đáp án

Lời giải

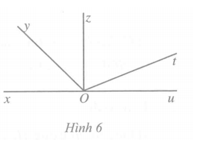
Ở hình 6, các cặp góc kề bù (khác góc bẹt) là: uOt và tOx, uOz và zOx, uOy và xOy.

Câu 3

Bạn Hoa cho rằng: “Nếu hai đường thẳng a và b cắt nhau tại O tạo thành bốn góc $\hat{O_{1}}, \hat{O_{2}}, \hat{O_{3}}, \hat{O_{4}}$ , như Hình 10 và trong số bốn góc đó có một góc vuông thì ta sẽ chứng tỏ được ba góc còn lại cũng là góc vuông”. Theo em, bạn Hoa nói đúng hay sai. Vì sao ?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Tìm các cặp góc kề nhau trong mỗi hình 5a, 5b:

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Hình 11 là một mẫu cửa có vòm tròn của một ngôi nhà. Nếu coi mỗi thanh chắn vòm cửa đó (ba thanh đánh số (1), (2), (3) trên hình) như một cạnh của góc thì các thanh chắn đó tạo ra các góc kề nhau. Theo em, mỗi góc tạo bởi hai thanh chắn vòm cửa đó khoảng bao nhiêu độ ?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

- Ở Hình 1, với điểm A bất kì trên tia Oz (A khác…), điểm B bất kì trên tia Ot (B khác …) thì đoạn thẳng AB luôn cắt ……………………… xy. Khi đó, hai tia Oz, Ot gọi là ……………………………………… đường thẳng xy.

- Ở Hình 2, hai góc xOy và zOy có O là ………………, tia Oy là ……………… và hai cạnh Ox, Oz nằm về …………………………………… cạnh chung Oy. Hai góc xOy và zOy như thế gọi là ………………………………………………………………………..

- Cho góc xOz (khác góc bẹt) và tia Oy nằm trong góc đó, tức là mỗi điểm M (M khác ...) của tia … đều là ……………………… của góc xOz. Khi đó, hai góc xOy và yOz là ……………………………………… và …………... = ……………+ ……………

- Nếu góc xOz là góc bẹt thì với mỗi tia Oy (khác hai tia Ox,….) , ta cũng có:

………….. = ………….. + …………….

- Hai góc bù nhau là hai góc …………………………………… 180°.

- Hai góc vừa ……………vừa ……………………………. kề bù (chẳng hạn, hai góc xOt và yOt ở Hình 3 là ……………………).

- Hai góc có một cạnh ……………., hai cạnh còn lại ………………………….. là ………………. kề bù.

- Hai góc đối đỉnh là …………………………………………………. của góc kia (chẳng hạn, hai góc xOy và zOt ở Hình 4 là ……………………………).

- Hai góc đối đỉnh thì ……….. nhau.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Vietjack official store

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

🔥 Đề thi HOT:

Bạn vui lòng để lại thông tin để được
TƯ VẤN THÊM

Hoặc gọi Hotline tư vấn: 084 283 45 85
Email: vietjackteam@gmail.com

VietJack