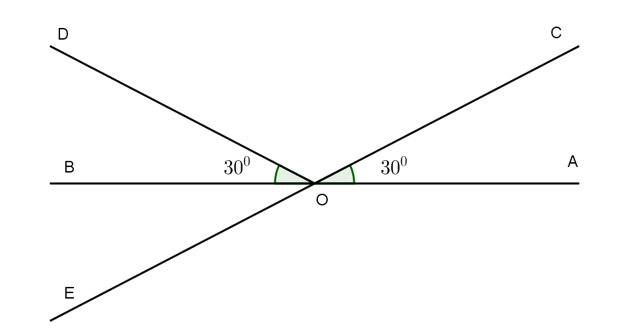
Cho hai đường thẳng AB và CD cắt nhau tại O sao cho = 43°. Khẳng định nào sau đây sai?
Cho hai đường thẳng AB và CD cắt nhau tại O sao cho = 43°. Khẳng định nào sau đây sai?
A. ;
B. ;
C. ;
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án đúng là: D
Hai đường thẳng AB và CD cắt nhau tại O nên OA là tia đối của tia OB, OC là tia đối của tia OD. Vậy và là 2 góc đối đỉnh ( Định nghĩa hai góc đối đỉnh ).
Nên = = 43°. Khẳng định A đúng. Khẳng định D sai.
Hai góc và có một cạnh chung OD, hai cạnh OA và OB là hai tia đối nhau nên và là hai góc kề bù ( Định nghĩa hai góc kề bù ).
Ta có + = 180° ( Tính chất hai góc kề bù )
⇒ = 180° = 137°. Khẳng định C đúng.
Hai đường thẳng AB và CD cắt nhau tại O nên OA là tia đối của tia OB, OC là tia đối của tia OD. Vậy và là 2 góc đối đỉnh ( Định nghĩa hai góc đối đỉnh ).
⇒ = = 137°. Khẳng định B đúng.
Vậy đáp án đúng là D.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. 125°;
B. 135°;
C. 55°;
D. 70°.
Lời giải

Lời giải
Hướng dẫn giải
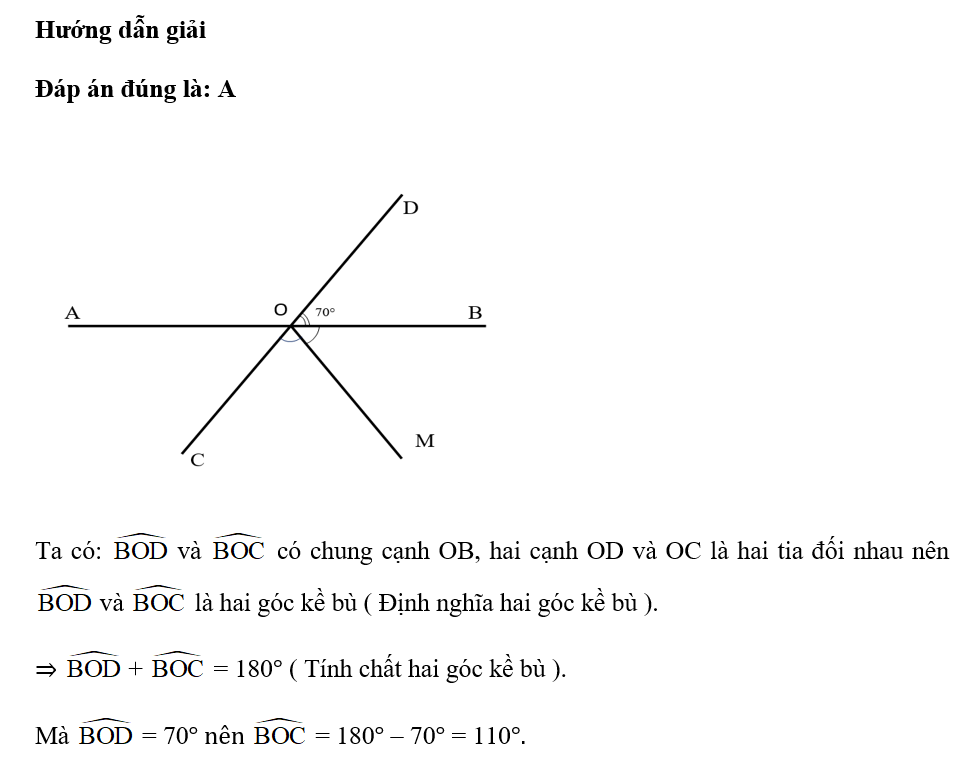
Đáp án đúng là: B
Hai đường thẳng AB và CD cắt nhau tại O nên OA là tia đối của tia OB, OC là tia đối của tia OD. Suy ra và là 2 góc đối đỉnh ( Định nghĩa hai góc đối đỉnh ).
Ta có = ( Tính chất hai góc đối đỉnh ).
Lại có:
mà ⇒ 6 = 180° ⇒ = 30° = .
Vậy = 30°. Đáp án đúng là B.
Câu 3
A. 30°;
B. 105°;
C. 125°;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. 120°;
B. 60°;
C. 30°;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. Góc đối đỉnh với là ;
B. Góc đối đỉnh với là ;
C. = ;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.