Cho ∆ABC vuông tại A. Kẻ AH vuông góc với BC (H ∈ BC). Các tia phân giác của ABC^ và HAC^ cắt nhau tại I. Khi đó ∆AIB là: A. Tam giác vuông tại I; B. Tam giác vuông tại B; C. Tam giác nhọn; D. Ta...

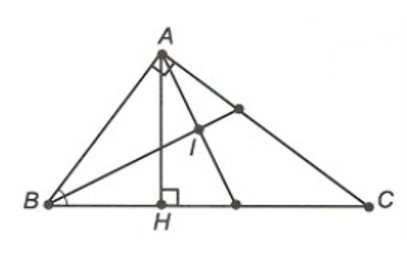
Hướng dẫn giải Đáp án đúng là: A ∆ABC vuông tại A: ABC^+ACB^=90° (hai góc phụ nhau) (1) ∆AHC vuông tại H: HAC^+ACH^=90° (hai góc phụ nhau) (2) Từ (1), (2), ta suy ra ABC^=HAC^. Ta có: ⦁ ABI^=12ABC^ (do BI là phân giác của ABC^); ⦁ HAI^=12HAC^ (do AI là phân giác của HAC^). Suy ra ABI^+HAI^=12ABC^+12HAC^=12HAC^+12HAC^=HAC^. ∆ABI có: ABI^+BAI^=ABI^+BAH^+HAI^ =ABI^+HAI^+BAH^=HAC^+BAH^=BAC^=90°. Mà ABI^+BAI^+AIB^=180° (định lí tổng ba góc trong một tam giác) Suy ra AIB^=180°−ABI^+BAI^=180°−90°=90°. Vậy ∆AIB vuông tại I. Do đó ta chọn phương án A.

Câu hỏi:

31/10/2022 1,295

Cho ∆ABC vuông tại A. Kẻ AH vuông góc với BC (H ∈ BC). Các tia phân giác của $\hat{A B C}$ và $\hat{H A C}$ cắt nhau tại I. Khi đó ∆AIB là:

A. Tam giác vuông tại I;

B. Tam giác vuông tại B;

C. Tam giác nhọn;

D. Tam giác tù.

Xem lời giải

Câu hỏi trong đề: Trắc nghiệm Tổng các góc trong một tam giác lớp 7 (có đáp án) !!

Quảng cáo

Trả lời:

Giải bởi Vietjack

Hướng dẫn giải

Đáp án đúng là: A

Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC (H thuộc BC). Các tia phân giác (ảnh 1)

∆ABC vuông tại A: $\hat{A B C} + \hat{A C B} = 90 °$ (hai góc phụ nhau) (1)

∆AHC vuông tại H: $\hat{H A C} + \hat{A C H} = 90 °$ (hai góc phụ nhau) (2)

Từ (1), (2), ta suy ra $\hat{A B C} = \hat{H A C}$ .

Ta có:

⦁ $\hat{A B I} = \frac{1}{2} \hat{A B C}$ (do BI là phân giác của $\hat{A B C}$ );

⦁ $\hat{H A I} = \frac{1}{2} \hat{H A C}$ (do AI là phân giác của $\hat{H A C}$ ).

Suy ra $\hat{A B I} + \hat{H A I} = \frac{1}{2} \hat{A B C} + \frac{1}{2} \hat{H A C} = \frac{1}{2} \hat{H A C} + \frac{1}{2} \hat{H A C} = \hat{H A C}$ .

∆ABI có: $\hat{A B I} + \hat{B A I} = \hat{A B I} + \hat{B A H} + \hat{H A I}$

$= (\hat{A B I} + \hat{H A I}) + \hat{B A H} = \hat{H A C} + \hat{B A H} = \hat{B A C} = 90 °$ .

Mà $\hat{A B I} + \hat{B A I} + \hat{A I B} = 180 °$ (định lí tổng ba góc trong một tam giác)

Suy ra $\hat{A I B} = 180 ° - (\hat{A B I} + \hat{B A I}) = 180 ° - 90 ° = 90 °$ .

Vậy ∆AIB vuông tại I.

Do đó ta chọn phương án A.

Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay

Các sản phẩm khác của Vietjack:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho ∆ABC có $\hat{A} = 75 °$ và $\hat{B} = 2 \hat{C}$ . Số đo của $\hat{C}$ bằng:

A. 70°;

B. 35°;

C. 40°;

D. 50°.

Lời giải

Hướng dẫn giải

Đáp án đúng là: B

∆ABC có: $\hat{A} + \hat{B} + \hat{C} = 180 °$ (định lí tổng ba góc trong một tam giác)

Suy ra $75 ° + 2 \hat{C} + \hat{C} = 180 °$ .

Do đó $3 \hat{C} = 180 ° - 75 ° = 105 °$ .

Vì vậy $\hat{C} = 105 ° : 3 = 35 °$ .

Vậy ta chọn phương án B.

Câu 2

Cho ∆ABC có $\hat{B} = 20 °$ , $\hat{C} = 40 °$ . Gọi AD là tia nằm giữa hai tia AB và AC sao cho $\hat{C A D} = 2 \hat{B A D}$ . Số đo của $\hat{A D C}$ bằng:

A. 10°;

B. 30°;

C. 45°;

D. 60°.

Lời giải

Hướng dẫn giải

Đáp án đúng là: D

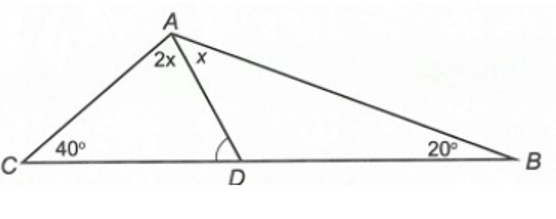
Cho tam giác ABC có góc B=20 độ; góc C=40 độ. Gọi AD là tia nằm giữa hai tia AB và AC sao cho (ảnh 1)

∆ABC có: $\hat{A} + \hat{B} + \hat{C} = 180 °$ (định lí tổng ba góc trong một tam giác)

Suy ra $\hat{A} = 180 ° - \hat{B} - \hat{C} = 180 ° - 20 ° - 40 ° = 120 °$ .

Gọi $x = \hat{B A D}$ (x > 0).

Suy ra $\hat{C A D} = 2 x$ .

Ta có $\hat{B A D} + \hat{C A D} = \hat{B A C} = 120 °$ .

Suy ra x + 2x = 120°.

Khi đó 3x = 120°.

Vì vậy x = 120° : 3 = 40°.

Suy ra $\hat{C A D} = 2 x = 2.40 ° = 80 °$ .

∆ACD có: $\hat{C A D} + \hat{A C D} + \hat{A D C} = 180 °$ (định lí tổng ba góc trong một tam giác)

Suy ra $\hat{A D C} = 180 ° - \hat{C A D} - \hat{A C D} = 180 ° - 80 ° - 40 ° = 60 °$ .

Vậy ta chọn phương án D.

Câu 3

Tam giác có một góc lớn hơn 90° là:

A. Tam giác nhọn;

B. Tam giác tù;

C. Tam giác vuông;

D. Đáp án khác.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho ∆ABC vuông tại B. Kết luận nào sau đây sai?

A. $\hat{A B C} = 90 °$ ;

B. $\hat{A} + \hat{C} = 90 °$ ;

C. $\hat{B} - \hat{C} = 90 °$ ;

\hat{C} = 90 ° - \hat{A}

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Hai góc phụ nhau là:

A. Hai góc có số đo không nhỏ hơn 90°;

B. Hai có tổng số đo bằng 180°;

C. Hai góc có giá trị tuyệt đối của hiệu số đo bằng 90°;

D. Hai góc có tổng số đo bằng 90°.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Kết luận nào sau đây đúng?

A. Một tam giác chỉ có tối đa hai góc nhọn;

B. Một tam giác chỉ có nhiều nhất một góc tù;

C. Trong một tam giác, có ít nhất hai góc có số đo nhỏ hơn 60°;

D. Trong một tam giác, số đo của mỗi góc luôn nhỏ hơn tổng số đo các góc còn lại.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Cho ∆ABC có $\hat{B} = 30 °, \hat{C} = 40 °$ . Khi đó ∆ABC là:

A. Tam giác tù;

B. Tam giác nhọn;

C. Tam giác vuông;

D. Đáp án khác.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Ôn vào 10

Ôn vào 6

V-ACT

HSA

TSA

SPT

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Khoa học tự nhiên

Tin học

Lịch sử

Địa lí

Toán

Văn

Tiếng Anh

Cho ∆ABC vuông tại A. Kẻ AH vuông góc với BC (H ∈ BC). Các tia phân giác của $\hat{A B C}$ và $\hat{H A C}$ cắt nhau tại I. Khi đó ∆AIB là:

Cho ∆ABC có $\hat{A} = 75 °$ và $\hat{B} = 2 \hat{C}$ . Số đo của $\hat{C}$ bằng:

Cho ∆ABC có $\hat{B} = 20 °$ , $\hat{C} = 40 °$ . Gọi AD là tia nằm giữa hai tia AB và AC sao cho $\hat{C A D} = 2 \hat{B A D}$ . Số đo của $\hat{A D C}$ bằng:

Cho ∆ABC có $\hat{B} = 30 °, \hat{C} = 40 °$ . Khi đó ∆ABC là: