3 câu Trắc nghiệm Tổng các góc trong một tam giác có đáp án (Vận dụng)
28 người thi tuần này 4.6 2.4 K lượt thi 3 câu hỏi 30 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
20 câu Trắc nghiệm Toán 7 Cánh Diều Ôn tập chương 5 (Đúng sai - Trả lời ngắn) có đáp án
44 lượt thi
20 câu hỏi
Danh sách câu hỏi:
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
Ta có:
⦁ (do MI là phân giác của );
⦁ (do PI là phân giác của ).
∆MIP có: (định lí tổng ba góc trong một tam giác)
Suy ra
(1)
∆MNP có: (định lí tổng ba góc trong một tam giác)
Suy ra (2)
Thế (2) vào (1) ta được: .
Vậy ta chọn phương án A.
Câu 2
A. 10°;
B. 30°;
C. 45°;
D. 60°.
Lời giải
Hướng dẫn giải
Đáp án đúng là: D
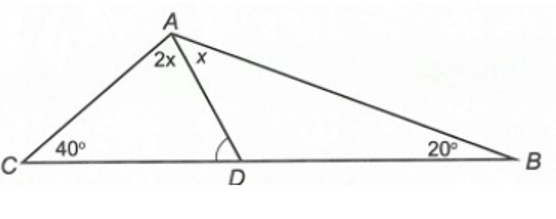
∆ABC có: (định lí tổng ba góc trong một tam giác)
Suy ra .
Gọi (x > 0).
Suy ra .
Ta có .
Suy ra x + 2x = 120°.
Khi đó 3x = 120°.
Vì vậy x = 120° : 3 = 40°.
Suy ra .
∆ACD có: (định lí tổng ba góc trong một tam giác)
Suy ra .
Vậy ta chọn phương án D.
Câu 3
A. Tam giác vuông tại I;
B. Tam giác vuông tại B;
C. Tam giác nhọn;
D. Tam giác tù.
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
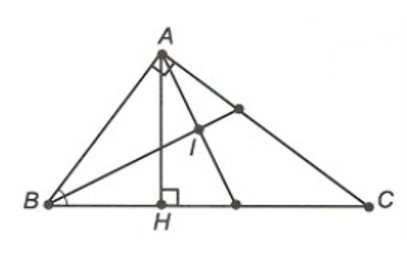
∆ABC vuông tại A: (hai góc phụ nhau) (1)
∆AHC vuông tại H: (hai góc phụ nhau) (2)
Từ (1), (2), ta suy ra .
Ta có:
⦁ (do BI là phân giác của );
⦁ (do AI là phân giác của ).
Suy ra .
∆ABI có:
.
Mà (định lí tổng ba góc trong một tam giác)
Suy ra .
Vậy ∆AIB vuông tại I.
Do đó ta chọn phương án A.
Nhắn tin Zalo
Hỏi bài tập