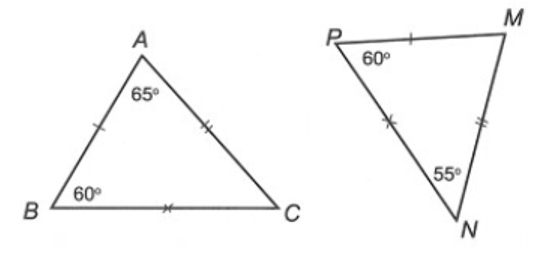
Cho ∆DEF và tam giác tạo bởi ba đỉnh M, N, P là hai tam giác bằng nhau. Biết rằng mỗi tam giác không có hai cạnh nào bằng nhau và không có hai góc nào bằng nhau. Biết và FD = PN. Cách kí hiệu nào sau đây đúng?
Cho ∆DEF và tam giác tạo bởi ba đỉnh M, N, P là hai tam giác bằng nhau. Biết rằng mỗi tam giác không có hai cạnh nào bằng nhau và không có hai góc nào bằng nhau. Biết và FD = PN. Cách kí hiệu nào sau đây đúng?
A. ∆DFE = ∆PMN;
B. ∆DEF = ∆MNP;
C. ∆DEF = ∆PMN;
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: C
Ta có (giả thiết)
Do đó D và P là hai đỉnh tương ứng.
Mà FD = PN.
Suy ra F và N là hai đỉnh tương ứng.
Từ đó ta có E và M là hai đỉnh tương ứng.
Vì vậy ta kí hiệu là: ∆DEF = ∆PMN.
Do đó ta chọn phương án C.
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
Ta có ∆ABC = ∆MNP (giả thiết)
Suy ra:
⦁ AB = MN; AC = MP và BC = NP (các cặp cạnh bằng nhau);
⦁ và (các cặp góc bằng nhau).
Vì AB = MN nên phương án A đúng.
Vì MP = AC nên phương án C đúng.
Vì nên phương án D đúng.
Vì vậy phương án B sai.
Do đó ta chọn phương án B.
Câu 2
A. AC = BC;
B. AC = DB;
C. BD = BC;
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
Xét ∆ABC và ∆DCB, có:
BC là cạnh chung.
AB = DC (giả thiết)
Do đó để ∆ABC = ∆DCB theo trường hợp cạnh – cạnh – cạnh thì cần thêm điều kiện về cạnh là AC = DB.
Vậy ta chọn phương án B.
Câu 3
A. ∆ABC = ∆DFE;
B. ∆ABC = ∆DEF;
C. ∆ABC = ∆EFD;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. ∆ABC = ∆KHI;
B. ∆ABC = ∆IKH;
C. ∆ABC = ∆HKI;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. ;
B. OM ⊥ AB;
C. OM là tia phân giác của ;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. ∆ABD = ∆BCD;
B. ∆BAD = ∆CDB;
C. ∆ABD = ∆CBD;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. BE = CD;
B. ∆ABE = ∆ACD;
C. ;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập