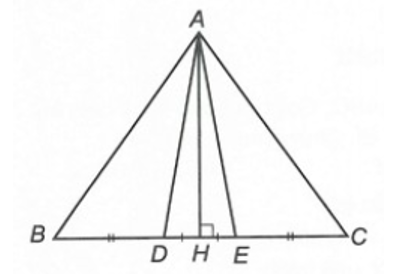
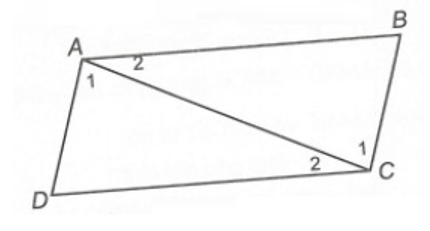
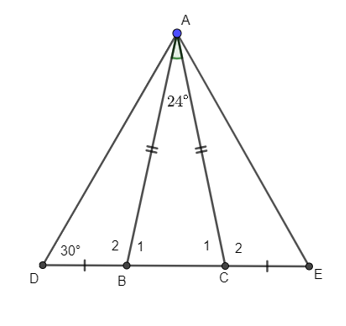
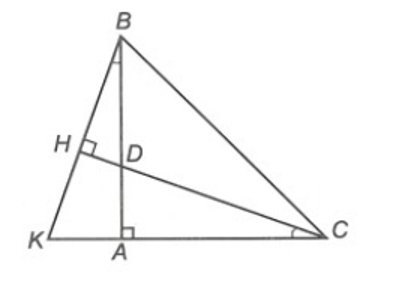
Cho hình vẽ bên. Biết rằng AB = AC. Kết luận nào sau đây đúng? A. ∆ABK = ∆ACD; B. AKB^≠ADC^; C. CD < BK; D. AK > AD.

Hướng dẫn giải Đáp án đúng là: A Xét ∆ABK và ∆ACD, có: AB = AC (giả thiết) BAK^=CAD^=90°. ABK^=ACD^ (giả thiết) Do đó ∆ABK = ∆ACD (g.c.g) Suy ra AKB^=ADC^, BK = CD và AK = AD (các cặp góc và cặp cạnh tương ứng) Vì vậy phương án A đúng, phương án B, C, D sai. Vậy ta chọn phương án A.

Câu hỏi:

31/10/2022 633

Cho hình vẽ bên. Biết rằng AB = AC.

Kết luận nào sau đây đúng?

A. ∆ABK = ∆ACD;

B. $\hat{A K B} \neq \hat{A D C}$ ;

C. CD < BK;

D. AK > AD.

Xem lời giải

Câu hỏi trong đề: 15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác có đáp án (Phần 2) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Hướng dẫn giải

Đáp án đúng là: A

Xét ∆ABK và ∆ACD, có:

AB = AC (giả thiết)

$\hat{B A K} = \hat{C A D} = 90 °$ .

$\hat{A B K} = \hat{A C D}$ (giả thiết)

Do đó ∆ABK = ∆ACD (g.c.g)

Suy ra $\hat{A K B} = \hat{A D C}$ , BK = CD và AK = AD (các cặp góc và cặp cạnh tương ứng)

Vì vậy phương án A đúng, phương án B, C, D sai.

Vậy ta chọn phương án A.

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho ∆ABC. Gọi I là trung điểm của AC. Trên tia đối của tia IB, lấy điểm E sao cho IE = IB. Khẳng định nào sau đây đúng?

A. AE = BC;

B. AE // BC;

C. ∆AIE = ∆CIB;

D. Cả A, B và C đều đúng.

Lời giải

Hướng dẫn giải

Đáp án đúng là: D

⦁ Xét ∆AIE và ∆CIB, có:

AI = CI (I là trung điểm của AC)

IE = IB (giả thiết)

$\hat{A I E} = \hat{B I C}$ (hai góc đối đỉnh)

Do đó ∆AIE = ∆CIB (c.g.c)

Vì vậy phương án C đúng.

⦁ Ta có ∆AIE = ∆CIB (chứng minh trên)

Suy ra AE = BC và $\hat{E A I} = \hat{I C B}$ (cặp cạnh và cặp góc tương ứng)

Vì vậy phương án A đúng.

⦁ Ta có $\hat{E A I} = \hat{I C B}$ (chứng minh trên)

Mà hai góc này ở vị trí so le trong.

Suy ra AE // BC.

Do đó phương án B đúng.

Vậy ta chọn phương án D.

Câu 2

Cho ∆ABC, điểm M thuộc cạnh BC. Đường thẳng đi qua M và song song với AB cắt AC ở D. Đường thẳng đi qua M và song song với AC cắt AB ở E.

Cho các khẳng định dưới đây:

(I) $\hat{A D M} = \hat{A E M}$ ;

(II) ME = AD;

(III) ∆AMD = ∆MAE.

Có bao nhiêu khẳng định đúng?

A. 0;

B. 1;

C. 2;

D. 3.

Lời giải

Hướng dẫn giải

Đáp án đúng là: D

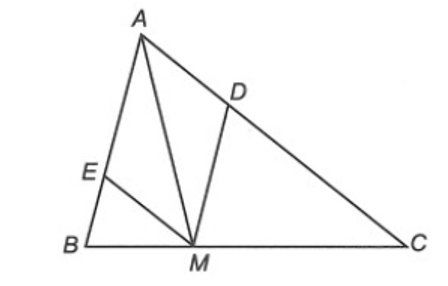
Cho tam giác ABC, điểm M thuộc cạnh BC. Đường thẳng đi qua M và song song (ảnh 1)

Xét ∆AMD và ∆MAE, có:

AM là cạnh chung.

$\hat{A M D} = \hat{M A E}$ (MD // AE)

$\hat{M A D} = \hat{A M E}$ (ME // AD)

Do đó ∆AMD = ∆MAE (g.c.g)

Suy ra ME = AD và $\hat{A D M} = \hat{A E M}$ (cặp cạnh và cặp góc tương ứng).

Do đó (I), (II), (III) đều đúng.

Vậy ta chọn phương án D.

Câu 3

Cho hình vẽ bên.

Có bao nhiêu cặp tam giác bằng nhau?

A. 1;

B. 2;

C. 3;

D. 4.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho hai tam giác ABC và DEF thỏa mãn AB = DE, $\hat{A B C} = \hat{DEF}$ , $\hat{B A C} = \hat{E D F}$ , AB = 5cm, AC = 6cm, EF = 8cm. Nửa chu vi p tam giác DEF nằm trong khoảng nào dưới đây:

A. 9 < p < 10;

B. 15 < p < 19;

C. 19 < p < 20;

D. 25 < p < 29.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho hình vẽ sau. Biết AB // CD và AD // BC.

Hình vẽ trên có mấy cặp tam giác bằng nhau?

A. 0;

B. 1;

C. 2;

D. 3.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho tam giác ABC cân tại A, có $\hat{A} = 24 °$ . Trên tia đối của tia BC lấy điểm D sao cho $\hat{A D B} = 30 °$ , trên tia đối của tia CB lấy điểm E sao cho BD = CE. Tính $\hat{B A E}$ ?

A. $\hat{A B E} = 72 °$ ;

B. $\hat{A B E} = 48 °$ ;

C. $\hat{A B E} = 78 °$ ;

\hat{A B E} = 68 °

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Cho hình vẽ bên. Biết rằng AB = AC. Kết luận nào sau đây đúng?

Cho ∆ABC. Gọi I là trung điểm của AC. Trên tia đối của tia IB, lấy điểm E sao cho IE = IB. Khẳng định nào sau đây đúng?

Cho hình vẽ bên. Có bao nhiêu cặp tam giác bằng nhau?

Cho hai tam giác ABC và DEF thỏa mãn AB = DE, ABC^=DEF^,BAC^=EDF^, AB = 5cm, AC = 6cm, EF = 8cm. Nửa chu vi p tam giác DEF nằm trong khoảng nào dưới đây:

Cho hình vẽ sau. Biết AB // CD và AD // BC. Hình vẽ trên có mấy cặp tam giác bằng nhau?

Cho tam giác ABC cân tại A, có A^=24°. Trên tia đối của tia BC lấy điểm D sao cho ADB^=30°, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Tính BAE^?

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho hình vẽ bên. Biết rằng AB = AC.

Kết luận nào sau đây đúng?

Cho hình vẽ bên.

Có bao nhiêu cặp tam giác bằng nhau?

Cho hai tam giác ABC và DEF thỏa mãn AB = DE, $\hat{A B C} = \hat{DEF}$ , $\hat{B A C} = \hat{E D F}$ , AB = 5cm, AC = 6cm, EF = 8cm. Nửa chu vi p tam giác DEF nằm trong khoảng nào dưới đây:

Cho hình vẽ sau. Biết AB // CD và AD // BC.

Hình vẽ trên có mấy cặp tam giác bằng nhau?

Cho tam giác ABC cân tại A, có $\hat{A} = 24 °$ . Trên tia đối của tia BC lấy điểm D sao cho $\hat{A D B} = 30 °$ , trên tia đối của tia CB lấy điểm E sao cho BD = CE. Tính $\hat{B A E}$ ?