Cho tập hợp L = {n| n = 2k + 1 với k ∈ ℕ}.
a) Nêu bốn số tự nhiên thuộc tập L và hai số tự nhiên không thuộc tập L;
b) Hãy mô tả tập L bằng cách nêu dấu hiệu đặc trưng theo một cách khác.
Cho tập hợp L = {n| n = 2k + 1 với k ∈ ℕ}.
a) Nêu bốn số tự nhiên thuộc tập L và hai số tự nhiên không thuộc tập L;
b) Hãy mô tả tập L bằng cách nêu dấu hiệu đặc trưng theo một cách khác.
Câu hỏi trong đề: Giải SBT Toán lớp 6 KNTT Bài 1: Tập hợp có đáp án !!
Quảng cáo
Trả lời:
L = {n| n = 2k + 1 với k ∈ ℕ}.
a)
+) Với k = 0, ta được: n = 2. 0 + 1 = 1 ∈ L
+) Với k = 1, ta được: n = 2. 1 + 1 = 3 ∈ L
+) Với k = 2, ta được: n = 2. 2 + 1 = 5 ∈ L
+) Với k = 3, ta được: n = 2. 3 + 1 = 7 ∈ L
Do đó bốn số tự nhiên thuộc tập L là: 1; 3; 5; 7
Vậy ta thấy hai số tự nhiên không thuộc tập L là: 0; 2
b)
Nhận thấy các số: 1; 3; 5; 7; ... là các số tự nhiên lẻ.
Tương tự với mọi số tự nhiên k thì ta tìm được các số n thuộc tập hợp L đều là các số tự nhiên lẻ.
Do đó ta có thể viết tập hợp L bằng cách nêu dấu hiệu đặc trưng khác như sau:
L = {n ∈ ℕ | n là các số lẻ}.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Các số tự nhiên n nhỏ hơn 20 và chia hết cho 5 là 0; 5; 10; 15.
Vì n thuộc M nên M = {0; 5; 10; 15}
Vậy M = {0; 5; 10; 15}.
Lời giải
Nhận xét:
+) Các phần tử trên giống nhau đều có tử bằng 1 vì 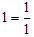
+) Các phần tử có mẫu số là các số tự nhiên lớn hơn 0 và nhỏ hơn 6 (hoặc nhỏ hơn hoặc bằng 5)
Do đó em có thể viết tập hợp M bằng một trong các cách sau:
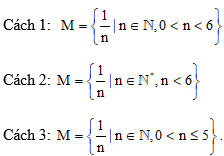
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
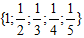 . Hãy mô tả tập hợp P bằng cách nêu dấu hiệu đặc trưng của các phần tử của nó.
. Hãy mô tả tập hợp P bằng cách nêu dấu hiệu đặc trưng của các phần tử của nó.