Câu hỏi:
12/07/2024 5,796
Từ một số tự nhiên n có ba chữ số cho trước, ta sẽ được số nào nếu:
a) Viết thêm chữ số 0 vào sau (tận cùng bên phải) số đó?
b) Viết thêm chữ số 1 vào trước (tận cùng bên trái) số đó?
Từ một số tự nhiên n có ba chữ số cho trước, ta sẽ được số nào nếu:
a) Viết thêm chữ số 0 vào sau (tận cùng bên phải) số đó?
b) Viết thêm chữ số 1 vào trước (tận cùng bên trái) số đó?
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Gọi số cần tìm là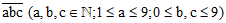 
Khi viết thêm chữ số 0 vào bên phải số đó ta được số: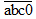 
Ta có: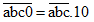 
Vậy nếu viết thêm chữ số 0 vào sau (tận cùng bên phải) số đó ta được số mới gấp 10 lần số đã cho.
b) Gọi số cần tìm là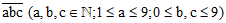
Khi viết thêm chữ số 1 vào trước (tận cùng bên trái) số đó ta được số: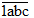 
Ta có: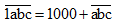 
Vậy nếu viết thêm chữ số 1 vào trước (tận cùng bên trái) số đó ta được số mới hơn số đã cho 1 000 đơn vị.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi chữ số hàng đơn vị của số cần tìm là a (a ∈ ℕ, 0 ≤ a ≤ 9)
Giả sử chữ số hàng đơn vị là 1, vì chữ số hàng chục lớn hơn chữ số hàng đơn vị là 9 do đó chữ số hàng chục là: 1 + 9 = 10, điều đó không xảy ra.
Nếu chữ số hàng đơn vị lớn hơn 1 thì chữ số hàng chục lớn hơn 10, điều đó không xảy ra.
Vì thế a = 0 hay chữ số hàng đơn vị là 0
Chữ số hàng chục là: 0 + 9 = 9
Vậy số cần tìm có hai chữ số là 90.
Lời giải
a) Vì số tự nhiên có ba chữ số và tập hợp các chữ số của nó là tập P nghĩa là số tự nhiên có ba chữ số khác nhau được tạo thành từ ba chữ số 0; 4; 9
Gọi số tự nhiên có ba chữ số khác nhau là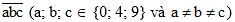 
Vì chữ số hàng trăm khác 0 nên a = 4 hoặc a = 9.
+) Với a = 4, ta có các số thỏa mãn là: 409; 490
+) Với a = 9, ta có các số thỏa mãn là: 904; 940
Vậy ta được các số thỏa mãn đề bài là: 409; 490; 904; 940.
b) Vì số tự nhiên có ba chữ số lấy trong tập P thì các số cần tìm được viết bởi 0; 4; 9 nhưng không nhất thiết có mặt cả ba chữ số đó. Vậy mỗi chữ số có thể không có mặt hoặc có mặt 1; 2 hoặc 3 lần.
Gọi số tự nhiên có ba chữ số là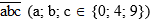 
Vì chữ số hàng trăm khác 0 nên a = 4 hoặc a = 9
Trường hợp 1: a = 4
+) Với a = 4, b = 0 ta có ba số: 400; 404; 409
+) Với a = 4, b = 4 ta được ba số: 440; 444; 449
+) Với a = 4, b = 9 ta được ba số: 490; 494; 499
Trường hợp 2: Với a = 9
+) Với a = 9, b = 0 ta được ba số: 900; 904; 909
+) Với a = 9; b = 4 ta được ba số: 940; 944; 949
+) Với a = 9, b = 9 ta được ba số: 990; 994; 999
Vậy các số thỏa mãn điều kiện đề bài là: 400; 404; 409; 440; 444; 449; 490; 494; 499; 900; 904; 909; 940; 944; 949; 990; 994; 999.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi Cuối học kì 2 Toán 6 có đáp án (Đề 1)
-
Đề kiểm tra Giữa kì 2 Toán 6 có đáp án (Mới nhất) - Đề 1
-
31 câu Trắc nghiệm Toán 6 Kết nối tri thức Bài 1: Tập hợp có đáp án
-
Dạng 1: Thực hiện tính, viết dưới dạng lũy thừa
-
Dạng 4: Một số bài tập nâng cao về lũy thừa
-
Đề thi Cuối học kì 2 Toán 6 có đáp án (Đề 2)
-
Dạng 4: Trung điểm của đoạn thẳng có đáp án
-
Dạng 1: tỉ số của hai đại lượng có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận