Câu hỏi:
13/07/2024 5,020
Tìm các số tự nhiên a và b (a < b), biết:
a) ƯCLN(a, b) = 15 và BCNN(a, b) = 180;
b) ƯCLN(a, b) = 11 và BCNN(a, b) = 484.
Tìm các số tự nhiên a và b (a < b), biết:
a) ƯCLN(a, b) = 15 và BCNN(a, b) = 180;
b) ƯCLN(a, b) = 11 và BCNN(a, b) = 484.
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Ta có: ab = ƯCLN(a, b). BCNN(a, b) = 15. 180 = 2 700.
Vì ƯCLN(a, b) = 15 nên a ⁝ 15, b ⁝ 15, ta giả sử a = 15m, b = 15 n. Do a < b nên m < n; m, n ∈ N* và ƯCLN(m, n) = 1.
Ta có: ab = 2 700
15m. 15n = 2 700
m. n. 225 = 2 700
m. n = 2 700: 225
m. n = 12 = 1. 12 = 2. 6 = 3. 4
Vì m và n là hai số nguyên tố cùng nhau, m < n và có tích là 12 nên ta có:
(m; n) ∈{(1; 12); (3; 4)}
+) Với (m; n) = (1; 12) thì a = 1. 15 = 15; b = 12. 15 = 180.
+) Với (m; n) = (3; 4) thì a = 3. 15 = 45; b = 4. 15 = 60.
Vậy các cặp (a; b) thỏa mãn là (15; 180); (45; 60).
b) Ta có: ab = ƯCLN(a, b). BCNN(a, b) = 11. 484 = 5 324.
Vì ƯCLN(a, b) = 11 nên , ta giả sử a = 11m, b = 11n. Do a < b nên m < n; m, n ∈ N* và ƯCLN(m, n) = 1.
Ta có: ab = 5 324
11m. 11n = 5 324
m. n. 121 = 5 324
m. n = 5 324: 121
m. n = 44 = 1. 44 = 4. 11
Vì m và n là hai số nguyên tố cùng nhau, m < n và có tích là 44 nên ta có:
(m; n) ∈{(1; 44); (4; 11)}
+) Với (m; n) = (1; 44) thì a = 1. 11 = 11; b = 44. 11 = 484.
+) Với (m; n) = (4; 11) thì a = 4. 11 = 44; b = 11. 11 = 121.
Vậy các cặp (a; b) thỏa mãn là (11; 484); (44; 121).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi số người trong buổi tập đồng diễn thể dục là x (người, x ∈ N*, 400 ≤ x ≤ 500)
Vì thầy tổng phụ trách xếp thành hàng 5 thì thừa 1 người nên x chia 5 dư 1 hay (x - 1) ⁝ 5
Vì thầy tổng phụ trách xếp thành hàng 6 thì thừa 1 người nên x chia 6 dư 1 hay (x - 1) ⁝ 6
Vì thầy tổng phụ trách xếp thành hàng 8 thì thừa 1 người nên x chia 8 dư 1 hay (x - 1) ⁝ 8
Do đó (x - 1) là bội chung của 5; 6 và 8.
Ta có: 5 = 5; 6 = 2. 3; 8 = 23
BCNN(5; 6; 8) = 23.3.5 = 120
(x - 1) B(120) = {0; 120; 240; 360; 480; 600;…}
Ta có bảng sau:
Mà buổi tập đồng diễn thể dục có khoảng 400 đến 500 người tham gia nên
Vì thế x = 481.
Vậy có chính xác 481 người dự buổi tập đồng diễn thể dục.
Lời giải
Vì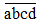 
là số có bốn chữ số chia hết cho cả 2; 5; 101 nên 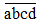là bội chung của 2; 5; 101.
Ta có: 2 = 2; 5 = 5; 101 = 101.
+) Không có thừa số nguyên tố chung và có thừa số riêng là 2; 5; 101.
+) Số mũ lớn nhất của 2 là 1, số mũ lớn nhất của 5 là 1, số mũ lớn nhất của 101 là 1
Khi đó BCNN(2, 5, 101) = 2. 5. 101 = 1 010.
Do đó 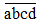∈ B(1 010) = {0; 1 010; 2 020; …}
Mà năm 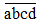thuộc thế kỉ XI nên 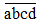= 1 010.
Vậy vua Lý Thái Tổ đã dời đô vào năm 1 010.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi Cuối học kì 2 Toán 6 có đáp án (Đề 1)
-
31 câu Trắc nghiệm Toán 6 Kết nối tri thức Bài 1: Tập hợp có đáp án
-
Dạng 4: Một số bài tập nâng cao về lũy thừa
-
Đề kiểm tra Giữa kì 2 Toán 6 có đáp án (Mới nhất) - Đề 1
-
10 câu Trắc nghiệm Toán 6 Chân trời sáng tạo Bài 1: Tập hợp. Phần tử của tập hợp (có đáp án)
-
Dạng 4: Trung điểm của đoạn thẳng có đáp án
-
Dạng 6: Bài tập vận dụng có đáp án
-
Đề kiểm tra Giữa kì 2 Toán 6 có đáp án (Mới nhất) - Đề 11