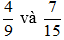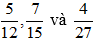Giải SGK Toán 6 KNTT Bài Luyện tập chung trang 54 - 55 có đáp án
35 người thi tuần này 4.6 1.5 K lượt thi 8 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi cuối kì 2 Toán 6 Kết nối tri thức có đáp án - Đề 10
Bộ 10 đề thi cuối kì 2 Toán 6 Kết nối tri thức có đáp án - Đề 09
Bộ 10 đề thi cuối kì 2 Toán 6 Kết nối tri thức có đáp án - Đề 08
Bộ 10 đề thi cuối kì 2 Toán 6 Kết nối tri thức có đáp án - Đề 07
Bộ 10 đề thi cuối kì 2 Toán 6 Kết nối tri thức có đáp án - Đề 06
Bộ 10 đề thi cuối kì 2 Toán 6 Kết nối tri thức có đáp án - Đề 05
Bộ 10 đề thi cuối kì 2 Toán 6 Kết nối tri thức có đáp án - Đề 04
Bộ 10 đề thi cuối kì 2 Toán 6 Kết nối tri thức có đáp án - Đề 03
Danh sách câu hỏi:
Lời giải
a)
+) Ở cột thứ hai:
a = 34 = 2.17; b = 51 = 3.17
⇒ ƯCLN(a; b) = 17 ; BCNN(a; b) = 2.3.17 = 102.
ƯCLN(a, b) . BCNN(a, b) = 17.102 = 1 734.
a.b = 34. 51 = 1 734.
+) Ở cột thứ ba:
a = 120 =23.3.5 ; b = 70 = 2.5.7
⇒ ƯCLN(a; b) = 2. 5 = 10 ; BCNN(a; b) = 23.3.5.7 = 840
ƯCLN(a, b) . BCNN(a, b) = 10. 840 = 8 400.
a.b = 120. 70 = 8 400.
+) Ở cột thứ tư:
a = 15 =3.5; b = 28 = 22.7
⇒ ƯCLN(a; b) = 1 ; BCNN(a; b) =
ƯCLN(a, b) . BCNN(a, b) =1. 420 = 420.
a.b = 15. 28 = 420.
+) Ở cột thứ năm:
a = 2 987; b = 1
⇒ ƯCLN(a; b) = 1 ; BCNN(a; b) = 2 987
ƯCLN(a, b) . BCNN(a, b) = 1 . 2 987 = 2 987.
a.b = 2 987 . 1 = 2 987
Ta có bảng sau:
|
a |
9 |
34 |
120 |
15 |
2 987 |
|
b |
12 |
51 |
70 |
28 |
1 |
|
ƯCLN(a, b) |
3 |
17 |
10 |
1 |
1 |
|
BCNN(a, b) |
36 |
102 |
840 |
420 |
2 987 |
|
ƯCLN(a, b) .BCNN(a, b) |
108 |
1 734 |
8 400 |
420 |
2 987 |
|
a.b |
108 |
1 734 |
8 400 |
420 |
2 987 |
b) So sánh: ƯCLN(a, b) . BCNN(a, b) = a.b
Em rút ra kết luận: tích của BCNN cà ƯCLN của hai số tự nhiên bất kì bằng tích của chúng.
Lời giải
a) 3.52 và 52.7
+) Ta thấy các thừa số nguyên tố chung là 5 và thừa số nguyên tố riêng là 3 và 7
+) Số mũ nhỏ nhất của 5 là 2 nên ƯCLN cần tìm là 52 = 25
+) Số mũ lớn nhất của 3 là 1, số mũ lớn nhất của 5 là 2, số mũ lớn nhất của 7 là 1 nên BCNN cần tìm là 3.52.7 = 525
Vậy ƯCLN cần tìm là 52 = 25
BCNN cần tìm là 3.52.7 = 525.
b) 22.3.5; 32.7 và 3.5.11
+) Ta thấy các thừa số nguyên tố chung là 3 và thừa số nguyên tố riêng là 2; 5; 7; 11
+) Số mũ nhỏ nhất của 3 là 1 nên ƯCLN cần tìm là 3
+) Số mũ lớn nhất của 2 là 2, số mũ lớn nhất của 3 là 2, số mũ lớn nhất của 5 là 1, số mũ lớn nhất của 7 là 1, số mũ lớn nhất của 11 là 1 nên BCNN cần tìm là 22.32.5.7.11 = 13 860
Vậy ƯCLN cần tìm là 3
BCNN cần tìm là 22.32.5.7.11 = 13 860.
Lời giải
a) Vì ƯCLN(15, 17) = 1 nên phân số 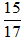 là phân số tối giản.
là phân số tối giản.
b) Ta có: 70 = 2.7.5; 105= 3.5.7
+) Thừa số nguyên tố chung là 5 và 7
+ Số mũ nhỏ nhất của 5 là 1, số mũ nhỏ nhất của 7 là 1 nên ƯCLN(70, 105) = 35.
Do đó 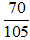 không là phân số tối giản
không là phân số tối giản
Ta có: 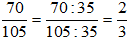 . Ta được
. Ta được 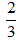 là phân số tối giản vì ƯCLN(2, 3) = 1.
là phân số tối giản vì ƯCLN(2, 3) = 1.
Lời giải
Đổi 360 giây = 6 phút, 420 giây = 7 phút
Giả sử sau x phút họ lại gặp nhau.
Vận động viên thứ nhất chạy một vòng sân hết 6 phút nên x là bội của 6.
Vận động viên thứ hai chạy một vòng sân hết 7 phút nên x là bội của 7.
Suy ra x ∈ BC(6; 7).
Mà x ít nhất nên x = BCNN(6; 7).
6 = 2.3; 7 = 7
x = BCNN(6; 7) = 2.3.7 = 42
Vậy sau 42 phút họ lại gặp nhau.
Lời giải
a) Ta có: 9 =32; 15 =3.5 nên BCNN(9, 15) = 32.5 = 45. Do đó ta có thể chọn mẫu chung là 45.
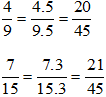
b) Ta có: 12 =22.3; 15 = 3.5 ; 27 = 33 nên BCNN(12, 15, 27) = 22.33.5 = 540. Do đó ta có thể chọn mẫu chung là 540.
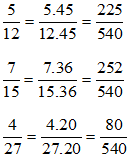
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.