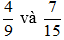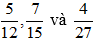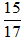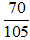Câu hỏi:
27/11/2022 1,269
Học sinh lớp 6A khi xếp thành hàng 2, hàng 3, hàng 7 đều vừa đủ hàng. Hỏi số học sinh lớp 6A là bao nhiêu, biết rằng số học sinh nhỏ hơn 45.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Học sinh lớp 6A khi xếp thành hàng 2, hàng 3, hàng 7 đều vừa đủ hàng.
Do đó số học sinh lớp 6A là BC(2, 3, 7)
BCNN(2, 3, 7) = 2.3.7 = 42 nên BC(2, 3, 7) = B(42) = {0; 42; 84, ...}
Mà số học sinh nhỏ hơn 45 nên số học sinh lớp 6A là 42.
Vậy số học sinh lớp 6A là 42 học sinh.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Ta có: 9 =32; 15 =3.5 nên BCNN(9, 15) = 32.5 = 45. Do đó ta có thể chọn mẫu chung là 45.
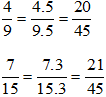
b) Ta có: 12 =22.3; 15 = 3.5 ; 27 = 33 nên BCNN(12, 15, 27) = 22.33.5 = 540. Do đó ta có thể chọn mẫu chung là 540.
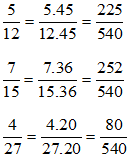
Lời giải
a)
+) Ở cột thứ hai:
a = 34 = 2.17; b = 51 = 3.17
⇒ ƯCLN(a; b) = 17 ; BCNN(a; b) = 2.3.17 = 102.
ƯCLN(a, b) . BCNN(a, b) = 17.102 = 1 734.
a.b = 34. 51 = 1 734.
+) Ở cột thứ ba:
a = 120 =23.3.5 ; b = 70 = 2.5.7
⇒ ƯCLN(a; b) = 2. 5 = 10 ; BCNN(a; b) = 23.3.5.7 = 840
ƯCLN(a, b) . BCNN(a, b) = 10. 840 = 8 400.
a.b = 120. 70 = 8 400.
+) Ở cột thứ tư:
a = 15 =3.5; b = 28 = 22.7
⇒ ƯCLN(a; b) = 1 ; BCNN(a; b) =
ƯCLN(a, b) . BCNN(a, b) =1. 420 = 420.
a.b = 15. 28 = 420.
+) Ở cột thứ năm:
a = 2 987; b = 1
⇒ ƯCLN(a; b) = 1 ; BCNN(a; b) = 2 987
ƯCLN(a, b) . BCNN(a, b) = 1 . 2 987 = 2 987.
a.b = 2 987 . 1 = 2 987
Ta có bảng sau:
|
a |
9 |
34 |
120 |
15 |
2 987 |
|
b |
12 |
51 |
70 |
28 |
1 |
|
ƯCLN(a, b) |
3 |
17 |
10 |
1 |
1 |
|
BCNN(a, b) |
36 |
102 |
840 |
420 |
2 987 |
|
ƯCLN(a, b) .BCNN(a, b) |
108 |
1 734 |
8 400 |
420 |
2 987 |
|
a.b |
108 |
1 734 |
8 400 |
420 |
2 987 |
b) So sánh: ƯCLN(a, b) . BCNN(a, b) = a.b
Em rút ra kết luận: tích của BCNN cà ƯCLN của hai số tự nhiên bất kì bằng tích của chúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi Cuối học kì 2 Toán 6 có đáp án (Đề 1)
-
Đề kiểm tra Giữa kì 2 Toán 6 có đáp án (Mới nhất) - Đề 1
-
31 câu Trắc nghiệm Toán 6 Kết nối tri thức Bài 1: Tập hợp có đáp án
-
Dạng 1: Thực hiện tính, viết dưới dạng lũy thừa
-
Dạng 4: Một số bài tập nâng cao về lũy thừa
-
Dạng 4: Trung điểm của đoạn thẳng có đáp án
-
Dạng 1: tỉ số của hai đại lượng có đáp án
-
Đề thi Cuối học kì 2 Toán 6 có đáp án (Đề 2)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận