Quảng cáo
Trả lời:
Giải bởi Vietjack
Theo mình, hai số không chia hết cho 4 thì tổng của chúng có thể chia hết cho 4 hoặc không chia hết cho 4.
Ví dụ: 5 và 7 là hai số không chia hết cho 4 nhưng (5 + 7) = 12 ⁝ 4
5 và 9 là hai số không chia hết cho 4 nhưng (5 + 9) = 14 
4
Vậy hai số không chia hết cho 4 thì chưa kết luận được tổng có chia hết cho 4 hay không.
Nhà sách vietjack
Hot: Đề thi cuối kì 2 Toán, Văn, Anh.... file word có đáp án chi tiết lớp 1-12 form 2025 (chỉ từ 100k). Tải ngay
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
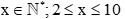
Đội thể thao của trường có 45 vận động viên. Huấn luyện viên muốn chia thành các nhóm để luyện tập sao cho mỗi nhóm có ít nhất 2 người và không quá 10 người. Biết rằng các nhóm có số người như nhau, em hãy giúp huấn luyện viên chia nhé.
Xem đáp án »
11/07/2024
28,659
Câu 2:
Tìm các số tự nhiên x, y sao cho:
a) x ∈ B(7) và x < 70
b) y ∈ Ư(50) và y > 5
Tìm các số tự nhiên x, y sao cho:
a) x ∈ B(7) và x < 70
b) y ∈ Ư(50) và y > 5
Xem đáp án »
11/07/2024
20,374
Câu 3:
Không thực hiện phép tính, hãy cho biết tổng nào sau đây chia hết cho 5?
a) 15 + 1 975 + 2 019;
b) 20 + 90 + 2 025 + 2 050.
Không thực hiện phép tính, hãy cho biết tổng nào sau đây chia hết cho 5?
a) 15 + 1 975 + 2 019;
b) 20 + 90 + 2 025 + 2 050.
Xem đáp án »
11/07/2024
14,996
Câu 4:
Không thực hiện phép tính, hãy cho biết hiệu nào sau đây chia hết cho 8?
a) 100 - 40
b) 80 - 16
Không thực hiện phép tính, hãy cho biết hiệu nào sau đây chia hết cho 8?
a) 100 - 40
b) 80 - 16
Xem đáp án »
11/07/2024
13,513
Câu 5:
Cô giáo muốn chia đều 40 học sinh để thực hiện các dự án học tập. Hoàn thành bảng sau vào vở (bỏ trống trong trường hợp không chia được)
Số nhóm
Số người ở một nhóm
4
?
?
8
6
?
8
?
?
4
Cô giáo muốn chia đều 40 học sinh để thực hiện các dự án học tập. Hoàn thành bảng sau vào vở (bỏ trống trong trường hợp không chia được)
|
Số nhóm |
Số người ở một nhóm |
|
4 |
? |
|
? |
8 |
|
6 |
? |
|
8 |
? |
|
? |
4 |
Xem đáp án »
11/07/2024
7,601
Câu 6:
a) Hãy tìm tất cả các ước của 20;
b) Hãy tìm tất cả các bội nhỏ hơn 50 của 4.
a) Hãy tìm tất cả các ước của 20;
b) Hãy tìm tất cả các bội nhỏ hơn 50 của 4.
Xem đáp án »
11/07/2024
2,628
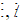) thay cho dấu “?”
🔥 Đề thi HOT:
-
Đề kiểm tra Giữa kì 2 Toán 6 có đáp án (Mới nhất) - Đề 1
-
Dạng 4: Một số bài tập nâng cao về lũy thừa
-
Đề kiểm tra Giữa kì 2 Toán 6 có đáp án (Mới nhất) - Đề 2
-
Đề thi Cuối học kì 2 Toán 6 có đáp án (Đề 1)
-
31 câu Trắc nghiệm Toán 6 Kết nối tri thức Bài 1: Tập hợp có đáp án
-
Dạng 5: Giải các bài toán thực tế có liên quan đến đoạn thẳng, độ dài đoạn thẳng và trung điểm của đoạn thẳng có đáp án
-
Dạng 1: tỉ số của hai đại lượng có đáp án
-
Đề kiểm tra Giữa kì 2 Toán 6 có đáp án (Mới nhất) - Đề 11
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận