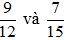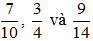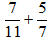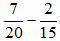Quảng cáo
Trả lời:
(1) a) 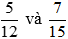
Ta có: 12 = 22.3; 15 = 3. 5 nên BCNN(12, 15) = 22.3.5 = 60
Ta có thể lấy mẫu chung của hai phân số trên là 60. Do đó:
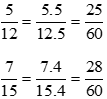
b)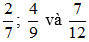
Ta có: 7 = 7; 9 = 32; 12 = 22.3 nên BCNN(7, 9, 12) = 22.32.7 = 252. Ta có thể lấy mẫu chung của hai phân số trên là 252
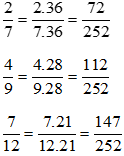
(2) a) 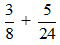
Vì 24 ⁝ 8 nên BCNN(8, 24) = 24. Do đó ta có thể lấy mẫu chung của hai phân số là 24 và:
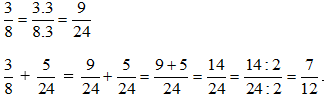
b)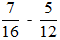 ;
;
Ta có: 16 = 24; 12 = 22.3 nên BCNN(16, 12) = 24.3 = 48. Do đó ta có thể lấy mẫu chung của hai phân số là 48
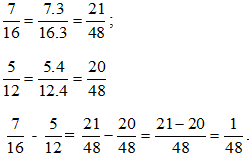
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Ta có BCNN(5; 7) = 5. 7 = 35 nên
BC(5; 7) = B(35) = {0; 35; 70; 105; 140; 175; 210; ...}
Vì bội chung nhỏ hơn 200 nên bội chung của 5 và 7 là: 0; 35; 70; 105; 140; 175
Vậy bội chung nhỏ hơn 200 của 5 và 7 là: 0; 35; 70; 105; 140; 175.
b) Ta có: 3 = 3; 4 = 22 10 = 2. 5.
Thừa số nguyên tố chung là 2 và riêng là 3 và 5.
Số mũ lớn nhất của 2 là 2, số mũ lớn nhất của 3 là 1, số mũ lớn nhất của 5 là 1
Khi đó BCNN(3, 4, 10) = 22.3.5 = 60.
BC(3; 4; 10) = B(60) = {0; 60; 120; 180; 240; ...}
Vì bội chung nhỏ hơn 200 nên bội chung của 3, 4 và 10 là 0; 60; 120; 180
Vậy bội chung nhỏ hơn 200 của 3, 4 và 10 là 0; 60; 120; 180.
Lời giải
a) Ta có: 12.22.3; nên BCNN(12, 15) = 22.3.5 = 60. Do đó ta có thể chọn mẫu chung là 60.
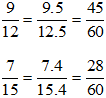
b) Ta có: 10 = 2.5; 4 = 22; 14 = 2. 7 nên BCNN(10, 4, 14) = 22.5.7 = 140. Do đó ta có thể chọn mẫu chung là 140
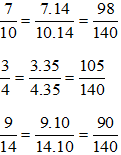
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.