Câu hỏi:
12/07/2024 514
Muốn tìm tập hợp ước chung chung của hai hay nhiều số tự nhiên, ta thực hiện:
A. Tìm ƯCLN của các số đó. Khi đó tập hợp ước chung của các số đó chính là tập hợp ước của ƯCLN.
B. Viết tập hợp các ước của các số đó ra. Tìm trong số đó các phần tử chung. Tập các phần tử đó chính là tập hợp ước chung của các số đó.
C. Cả A và B đều sai.
D. Cả A và B đều đúng.
Muốn tìm tập hợp ước chung chung của hai hay nhiều số tự nhiên, ta thực hiện:
A. Tìm ƯCLN của các số đó. Khi đó tập hợp ước chung của các số đó chính là tập hợp ước của ƯCLN.
B. Viết tập hợp các ước của các số đó ra. Tìm trong số đó các phần tử chung. Tập các phần tử đó chính là tập hợp ước chung của các số đó.
C. Cả A và B đều sai.
D. Cả A và B đều đúng.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Muốn tìm tập hợp ước chung chung của hai hay nhiều số tự nhiên, ta có hai cách để tìm như sau:
Cách 1.
- Tìm ƯCLN của các số đó.
- Tìm các ước của ƯCLN đó.
- Kết luận tập hợp ƯC là tập các ước của ƯCLN.
Cách 2.
- Liệt kê tập hợp ước của các số.
- Tìm các phần tử chung của các tập hợp đó.
- Tập hợp ƯC là tập các phần tử chung đó.
Vậy cả A và B đều đúng.
Đáp án: D
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Phân tích a và b ra thừa số nguyên tố
Ta có:
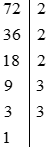
Do đó: a = 72 = 23.32.
Lại có:
Vậy b = 96 = 25.3.
b) Ta thấy 2 và 3 là các thừa số chung của 70 và 96. Số mũ nhỏ nhất của 2 là 3 và số mũ nhỏ nhất của 3 là 1 nên
ƯCLN(72; 96) = 23 . 3 = 24
ƯC(a, b) = Ư(24) = {1; 2; 3; 4; 6; 8; 12; 24}.
Lời giải
a) Ta có:
50 = 2.52; 85 = 5.17
+) Thừa số nguyên tố chung là 5 với số mũ nhỏ nhất là 1 nên ƯCLN(50, 85) = 5.
Do đó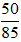 
không là phân số tối giản.
. Ta được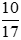 
là phân số tối giản vì ƯCLN(10, 17) = 1.
b) Ta có:
23 = 23; 81 = 34
Nên 23 và 81 không có thừa số nguyên tố chung nên ƯCLN(23, 81) = 1.
Do đó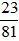 
là phân số tối giản.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi Cuối học kì 2 Toán 6 có đáp án (Đề 1)
-
31 câu Trắc nghiệm Toán 6 Kết nối tri thức Bài 1: Tập hợp có đáp án
-
Dạng 4: Một số bài tập nâng cao về lũy thừa
-
Đề kiểm tra Giữa kì 2 Toán 6 có đáp án (Mới nhất) - Đề 1
-
10 câu Trắc nghiệm Toán 6 Chân trời sáng tạo Bài 1: Tập hợp. Phần tử của tập hợp (có đáp án)
-
Dạng 4: Trung điểm của đoạn thẳng có đáp án
-
Dạng 6: Bài tập vận dụng có đáp án
-
Đề kiểm tra Giữa kì 2 Toán 6 có đáp án (Mới nhất) - Đề 11