Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: D
Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn; góc đối diện với cạnh nhỏ hơn là góc nhỏ hơn.
Trong một tam giác vuông, cạnh huyền là cạnh lớn nhất.
Trong một tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất.
Vậy ta chọn phương án D.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
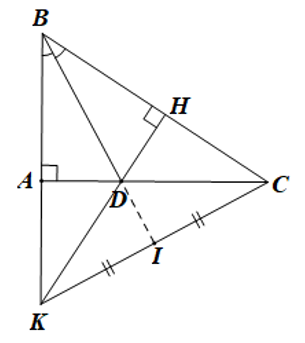
a) Xét ∆ABD và ∆HBD có
BD là cạnh chung
(do BD là tia phân giác của góc ABD)
Do đó ΔABD = ΔHBD (cạnh huyền – góc nhọn).
b) Từ ΔABD = ΔHBD (câu a) suy ra AD = HD (hai cạnh tương ứng)
Xét ΔDHC vuông tại H có DC là cạnh huyền nên DC là cạnh lớn nhất
Do đó DC > HD nên DC > AD.
c) Xét ΔBKC có CA ⊥ BK, KH ⊥ BC và CA cắt KH tại D
Do đó D là trực tâm của ΔBKC, nên BD ⊥ KC (1)
Gọi J là giao điểm của BD và KC.
Xét ΔBKJ và ΔBCJ có:
BJ là cạnh chung,
(do CJ là tia phân giác của góc ABD)
Do đó ΔBKJ = ΔBCJ (cạnh góc vuông – góc nhọn kề)
Suy ra KJ = CJ (hai cạnh tương ứng)
Hay J là trung điểm của KC.
Mà theo bài I là trung điểm của KC nên I và J trùng nhau.
Do đó ba điểm B, D, I thẳng hàng.
Lời giải
Giải:
Gọi số công nhân tham gia làm việc của đội thứ nhất, đội thứ hai, đội thứ ba lần lượt là x, y, z.
Số công nhân của đội thứ ba ít hơn số công nhân của đội thứ hai là 5 người nên y – z = 5.
Với cùng một khối lượng công việc, số công nhân tham gia làm việc và thời gian hoàn thanh công việc của mỗi đội là hai đại lượng tỉ lệ nghịch với nhau.
Do đó, ta có 2x = 3y = 4z suy ra \(\frac{x}{{\frac{1}{2}}} = \frac{y}{{\frac{1}{3}}} = \frac{z}{{\frac{1}{4}}}\).
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\frac{x}{{\frac{1}{2}}} = \frac{y}{{\frac{1}{3}}} = \frac{z}{{\frac{1}{4}}} = \frac{{y - z}}{{\frac{1}{3} - \frac{1}{4}}} = \frac{5}{{\frac{1}{{12}}}} = 60\).
Từ đó suy ra \(x = 60.\frac{1}{2} = 30\), \(y = 60.\frac{1}{3} = 20\), \(z = 60.\frac{1}{4} = 15\).
Vậy số công nhân tham gia làm việc của đội thứ nhất, đội thứ hai, đội thứ ba lần lượt là 30 người, 20 người, 15 người.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo