Cho đường tròn O, bán kính R. Từ một điểm M ở ngoài đường tròn (O) sao cho MO = 2R, ta kẽ hai tiếp tuyến MA và MB (A và B là tiếp điểm). Một cát tuyến bất kỳ qua M cắt đường tròn tại C và D . Kẻ tia phân giác của cắt dây CD tại E và đường tròn tại N.
a).Chứng minh tứ giác OAMB nội tiếp được.
Cho đường tròn O, bán kính R. Từ một điểm M ở ngoài đường tròn (O) sao cho MO = 2R, ta kẽ hai tiếp tuyến MA và MB (A và B là tiếp điểm). Một cát tuyến bất kỳ qua M cắt đường tròn tại C và D . Kẻ tia phân giác của cắt dây CD tại E và đường tròn tại N.
a).Chứng minh tứ giác OAMB nội tiếp được.
Câu hỏi trong đề: Đề thi Học kì 1 Toán 9 có đáp án năm 2022-2023 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
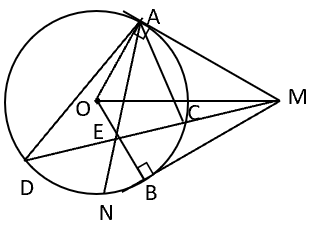
a) Vì MA và MB là hai tiếp tuyến nên MAOA, MB OB nên
+ = 900 + 900 = 1800 => OAMB là tứ giác nội tiếpHot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi x km/h là vận tốc của ôtô thưa nhất, điều kiện x > 12
Vận tốc của ôtô thứ hai là x -12 km/h.
Thời gian ôtô thứ nhất đi từ A đến B (giờ)
Thời gian ôtô thứ hai đi từ A đến B (giờ)
Vì ôtô thứ nhất đến nơi sớm hơn ôtô thứ hai 30 phút = giờ nên ta có phương trình
Rút gọn phương trình ta được: x2 - 12x - 2880 = 0
Giải ra ta được x1 = 60 (nhận), x2 = -48 (loại)
Vậy vận tốc của xe thứ nhất là 60 km/h, vận tốc của xe thứ hai là 60 - 12 = 48 km/h
Lời giải
Vậy hệ pt có nghiệm duy nhất (x,y) = (1,2)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo