Cho hình bình hành ABCD có AB = 2AD. Gọi E, F thứ tự là trung điểm của AB và CD
a) Các tứ giác AEFD, AECF là hình gì? Vì sao?
b) Gọi M là giao điểm của AF và DE, gọi N là giao điểm của BF và CE. Chứng minh rằng tứ giác EMFN là hình chữ nhật.
Cho hình bình hành ABCD có AB = 2AD. Gọi E, F thứ tự là trung điểm của AB và CD
a) Các tứ giác AEFD, AECF là hình gì? Vì sao?
b) Gọi M là giao điểm của AF và DE, gọi N là giao điểm của BF và CE. Chứng minh rằng tứ giác EMFN là hình chữ nhật.
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
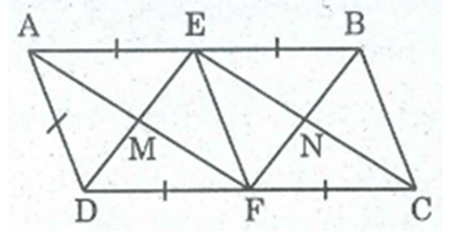
a) Ta có: \(AE = DE = \frac{1}{2}AB\) và AE // DF
→ tứ giác AEFD là hình bình hành
Có thêm \(AE = AD = \frac{1}{2}AB\)
→AEFD là hình thoi (dấu hiệu nhận biết hình thoi)
AE // FC và AE = FC ( vì cùng \( = \frac{1}{2}AB\))
→ AECF là hình bình hành
b) Tứ giác AECF là hình bình hành nên EN // MF(1)
Chứng minh tương tự câu a tứ giác EBFN là hình bình hành
→ ME // FN(2)
Từ (1) và (2) suy ra EMFN là hình bình hành (3)
Tứ giác AEFD là hình thoi nên suy ra \[{\rm{AF}} \bot DE\]
\( \to \widehat {{\rm{EMF}}} = {90^ \circ }\) (4)
Từ (3) và (4) suy ra EMFN là hình chữ nhật
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
O là số chính phương. Vì số chính phương là số có thể lấy căn bậc 2. Kết quả phải là số nguyên. Căn bậc 2 của 0 = 0
1 là số chính phương. Vì số chính phương là số có thể lấy căn bậc 2. Kết quả phải là số nguyên. Căn bậc 2 của 1 = 1
Lời giải
Hai góc tương ứng là hai góc của hai tam giác khác nhau.
Hai góc đó bằng nhau và nằm trong hai tam giác bằng nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \[{\rm{3}}\overrightarrow {{\rm{IM}}} {\rm{ + 4}}\overrightarrow {{\rm{IN}}} {\rm{ + }}\overrightarrow {{\rm{IP}}} {\rm{ = }}\overrightarrow {\rm{0}} \]
B. \[\overrightarrow {{\rm{IM}}} {\rm{ + 3}}\overrightarrow {{\rm{IN}}} {\rm{ + 4}}\overrightarrow {{\rm{IP}}} {\rm{ = }}\overrightarrow {\rm{0}} \]
C. \[{\rm{4}}\overrightarrow {{\rm{IM}}} {\rm{ + 3}}\overrightarrow {{\rm{IN}}} {\rm{ + }}\overrightarrow {{\rm{IP}}} {\rm{ = }}\overrightarrow {\rm{0}} \]
D. \[{\rm{4}}\overrightarrow {{\rm{IM}}} {\rm{ + }}\overrightarrow {{\rm{IN}}} {\rm{ + 3}}\overrightarrow {{\rm{IP}}} {\rm{ = }}\overrightarrow {\rm{0}} \]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập
Hà Thanh
CC